DSPy¶
Indice¶
Introduzione Indice
Questo Notebook vuole fornire un percorso didattico per illustrare l'applicazione del linguaggio Python nel realizzare la tecniche fondamentali per la sintesi, elaborazione ed analisi del suono.
Lo scopo è un approfondimento teorico su alcuni concetti che stanno alla base dell'informatica musicale e non applicativo o performativo, per questo motivo tutti i suoni saranno sintetizzati in tempo differito e memorizzati in sound files che potranno essere importabili in una qualsiasi delle principali DAW.
Alcuni dei concetti e strumenti informatici persenti sono tratti da Think DSP di Allen B. Downey - O'Reilly media.
Prerequisiti Indice
- Familiarità con la programmazione in Python (METTI LINK AL NOTEBOOK).
- Familiarità con il paradigma di programmazione orientata agli oggetti (METTI LINK AL NOTEBOOK).
- Familiarità con i principali concetti legati all'informatica musicale e alla programmazione di strumenti virtuali (campioni, rata di campionamento, inviluppoi, segnali di controllo, etc.).
- Familiarità con concetti base di matematica inclusi i numeri complessi.
Installazione Indice
Scarichiamo ed installiamo:
- Python (Anaconda distribution)
- VScode (Incluso con l'Anaconda distribution)
Saranno utilizzate inoltre le seguenti librerie (se si utilizza Anaconda sono già tutte presenti nella distribuzione, altrimenti bisogna scaricarle).
import copy
import math
import numpy as np
import random
import scipy
import scipy.stats
import scipy.fftpack
import subprocess
import warnings
from wave import open as open_wave
from scipy.io import wavfile
import matplotlib.pyplot as plt
try:
from IPython.display import Audio
except:
warnings.warn(
"Non posso importare IPython.display; " "Wave.make_audio() non funzionerà."
)
import os
import sys
path = os.path.abspath('moduli') # Restituisce il path assoluto della cartella
sys.path.insert(0, path) # Aggiunge la cartella moduli alla directory di lavoro
import pym # Importa il modulo custom
PI2 = math.pi*2 # Costante
Risorse in rete Indice
Primo promemoria (dominio del tempo)Indice
Il suono è formato da piccole variazioni della pressione atmosferica che si propagano nel tempo e nello spazio (onda sonora).
Un segnale audio rappresenta dunque una grandezza che varia nel tempo.
Le variazioni di pressione atmosferica possono essere misurate da un microfono che le trasduce in segnali elettrici (variazione di tensione).
I segnali elettrici (continui) possono essere campionati attraverso un dispositivo (adc) che li trasforma in segnali digitali (discreti).
Un segnale audio digitale è dunque rappresentato attraverso una sequenza di valori equispaziati nel tempo (numeric stream).
Questi valori si chiamano campioni (samples) e definiscono le ampiezze istantanee del segnale.
Per convenzione sono compresi tra +1.0 e -1.0.
Gli istanti di tempo in cui sono misurati i campioni si chiamano frames.
I termini samples e frames a volte sono impiegati come sinonimi.
Possiamo sintetizzare un segnale audio digitale calcolando attraverso una funzione d'onda i valori dei campioni (ys) per ogni frame consecutivo (ts).
I valori ottenuti (discreti) possono essere inviati a un dispositivo (dac) che li trasforma in segnale elettrico (continuo) il quale può fornire l'energia necessaria alla generazione del movimento della membrana di un altoparlante che a sua volta produce variazioni di pressione atmosferica (suono).
La quantità di campioni misurati o generati in un secondo si chiama rata di campionamento (sample rate o frame rate).
In Python possiamo memorizzare questi valori sotto forma di numpy.ndarray che ci facilitano la computazione di operazioni matematiche su tutti gli elementi della lista senza la necessità di iterarli.
framerate = 11025
nf = np.arange(0,100, 1) # Ganera gli indici dei frames np.arange(inizio,fine,passo)
ts = nf / framerate # Array di frames
ys = np.sin(PI2 * 111 * ts + 0) # Array di campioni (funzione d'onda della sinusoide)
print(nf)
print(ts)
plt.plot(ys, 'b:')
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99] [0.00000000e+00 9.07029478e-05 1.81405896e-04 2.72108844e-04 3.62811791e-04 4.53514739e-04 5.44217687e-04 6.34920635e-04 7.25623583e-04 8.16326531e-04 9.07029478e-04 9.97732426e-04 1.08843537e-03 1.17913832e-03 1.26984127e-03 1.36054422e-03 1.45124717e-03 1.54195011e-03 1.63265306e-03 1.72335601e-03 1.81405896e-03 1.90476190e-03 1.99546485e-03 2.08616780e-03 2.17687075e-03 2.26757370e-03 2.35827664e-03 2.44897959e-03 2.53968254e-03 2.63038549e-03 2.72108844e-03 2.81179138e-03 2.90249433e-03 2.99319728e-03 3.08390023e-03 3.17460317e-03 3.26530612e-03 3.35600907e-03 3.44671202e-03 3.53741497e-03 3.62811791e-03 3.71882086e-03 3.80952381e-03 3.90022676e-03 3.99092971e-03 4.08163265e-03 4.17233560e-03 4.26303855e-03 4.35374150e-03 4.44444444e-03 4.53514739e-03 4.62585034e-03 4.71655329e-03 4.80725624e-03 4.89795918e-03 4.98866213e-03 5.07936508e-03 5.17006803e-03 5.26077098e-03 5.35147392e-03 5.44217687e-03 5.53287982e-03 5.62358277e-03 5.71428571e-03 5.80498866e-03 5.89569161e-03 5.98639456e-03 6.07709751e-03 6.16780045e-03 6.25850340e-03 6.34920635e-03 6.43990930e-03 6.53061224e-03 6.62131519e-03 6.71201814e-03 6.80272109e-03 6.89342404e-03 6.98412698e-03 7.07482993e-03 7.16553288e-03 7.25623583e-03 7.34693878e-03 7.43764172e-03 7.52834467e-03 7.61904762e-03 7.70975057e-03 7.80045351e-03 7.89115646e-03 7.98185941e-03 8.07256236e-03 8.16326531e-03 8.25396825e-03 8.34467120e-03 8.43537415e-03 8.52607710e-03 8.61678005e-03 8.70748299e-03 8.79818594e-03 8.88888889e-03 8.97959184e-03]
[<matplotlib.lines.Line2D at 0x15223f3d0>]
Architettura informaticaIndice
Secondo quanto ricordato nel promemoria cominciamo a formalizzare un insieme di classi (modulo) seguendo il paradigma della programmazione orientata agli oggetti (OOP).
N.B. Nel corso del notebook le classi saranno di volta volta aggiornate con nuove funzionalità e sostituiranno le versioni precedenti. Il modulo nella sua versione finale può essere scaricato a questo link (METTI LINK!!!!!!!!).
WaveIndice
Cominciamo col definire la classe Wave che rappresenta una forma d'onda generica discreta e accetta come proprietà:
- una collezione di campioni (ys).
- una collezione di frames (ts).
- una rata di campionamento (framerate).
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys) # converte qualsiasi tipo di collezione
# in un ndarray
self.framerate = framerate if framerate is not None else 11025 # framerate di default = 11025
if ts is None: # Se non specifichiamo i frames
self.ts = np.arange(len(ys)) / self.framerate # li calcola dal numero di campioni
else:
self.ts = np.asanyarray(ts)
def __len__(self): # Riporta il numero di frames (dunder method)
return len(self.ys)
@property # Riporta il valore del primo frame
def start(self):
return self.ts[0]
@property # Riporta li valore dell'ultimo frame
def end(self):
return self.ts[-1]
@property
def duration(self): # Calcola e riporta la durata in secondi (float)
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs): # Se ys sono numeri complessi, visualizza la parte reale.
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs) # options
def plot_vlines(self,curva="linear",**kvargs): # Plot con linee verticali
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
Notiamo l'utilizzo di np.asanyarray() che accetta come argomento qualsiasi tipo di collezione (tuple, list, dict, etc.) ed esegue il casting in np.ndarray().
Notiamo l'attributo curva dei plot che definisce la visualizzazione degli assi lineare (default) o logaritmica.
Notiamo l'attributo **kwargs che definisce gli stili del plot.
Un introduzione a pyplot la troviamo qui.
Per verificare le funzionalità utilizziamo come proprietà gli stessi parametri già espressi alla fine del promemoria.
framerate = 11025
nf = np.arange(0,100, 1) # Ganera gli indici dei frames np.arange(inizio,fine,passo)
ts = nf / framerate # Array di frames
ys = np.sin(PI2 * 111 * ts + 0) # Array di campioni (funzione d'onda della sinusoide)
a = pym.Wave(ys,ts,framerate) # Istanza
print('len:', len(a)) # Capacità
print('start:', a.start) # Getters (Decoratori)
print('end:', a.end)
print('dur:', a.duration)
len: 100 start: 0.0 end: 0.008979591836734694 dur: 0.009070294784580499
a.plot(color="red",linewidth=1,linestyle='dotted') # Plot normale
a.plot_vlines(color="red",linewidth=1,linestyle='dotted') # Plot con barre verticali
SignalIndice
Definiamo ora una SuperClasse chiamata Signal che provvederà a fornire funzionalità comuni ai diversi tipi di segnale.
- generare un plot del segnale (per le forme d'onda periodiche visualizza 3 cicli di default).
- generare un'istanza di Wave.
class Signal:
"""
Rappresenta un segnale nel tempo.
"""
# ==================================== Questo metodo sarà spiegato nel paragrafo sulla sintesi additiva
def __add__(self, other):
"""Somma due segnali.
other: Signal
returns: Signal
"""
if other == 0:
return self
return SumSignal(self, other) # Richiama la classe SumSignal()
__radd__ = __add__
# ====================================
@property # Decoratore
def period(self): # Restituisce il periodo in secondi
"""
principalmente per i plot dei segnali
returns: secondi - float
"""
return 0.1
def plot(self, framerate=11025): # Genera un Plot del segnale
duration = self.period * 3 # Default 3 periodi
wave = self.make_wave(duration, start=0, framerate=framerate)
wave.plot()
def make_wave(self, duration=1, start=0, framerate=11025): # Crea un'istanza di Wave
"""
duration: float seconds
start: float seconds
framerate: int frames per second
returns: Wave
"""
n = round(duration * framerate) # Durata in frames
ts = start + np.arange(n) / framerate # Genera ts (come nel codice precedente)
ys = self.evaluate(ts) # Valuterà le singole funzioni d'onda definite nelle sottoclassi
return Wave(ys, ts, framerate=framerate)
Notiamo alla penultima linea la presenza di evaluate(ts) che richiama una funzione vuota.
Questa sarà definita di volta in volta nelle sottoclassi a seconda della funzione d'onda di generazione dei valori ys.
Il metodo make_wave() restituisce un'istanza della classe Wave.
SinusoidIndice
Definiamo ora una sottoclasse chiamata Sinusoid() che eredita i metodi di Signal() e genera ys e ts al suo interno a seconda delle proprietà che specifichiamo.
class Sinusoid(Signal):
"""Rappresenta un segnale sinusoidale"""
def __init__(self, freq=440, amp=1.0, offset=0, func=np.sin):
"""
freq: float frequency in Hz
amp: float amplitude, 1.0 is nominal max
offset: float phase offset in radians
func: function that maps phase to amplitude
"""
self.freq = freq
self.amp = amp
self.offset = offset
self.func = func
@property
def period(self): # Restituisce il periodo in secondi
return 1.0 / self.freq
def evaluate(self, ts): # Definisce la funzione evaluate che viene richiamata
ts = np.asarray(ts) # dalla SuperClasse Signal
phases = PI2 * self.freq * ts + self.offset
ys = self.amp * self.func(phases)
return ys
a = pym.Sinusoid(600, 0.6, 0) # Istanza di Sinusoid (freq amp fase)
print(a.period) # Periodo in secondi
a.plot() # Plot di Signal
0.0016666666666666668
Possiamo generare un oggettto Wave e invocare i suoi metodi.
b = a.make_wave(a.period * 2) # Crea un'istanza di Wave - Durata in secondi
b.plot_vlines(color="red",linewidth=1,linestyle='dotted') # Plot con barre verticali (invocato su Wave)
Definiamo alcune funzionalità che potrebbero tornare utili aggiungendo metodi alla classe Wave.
- wave.shift() - slitta la forma d'onda a sinistra o a destra nel tempo (secondi).
- wave.roll() - slitta la forma d'onda di un numero di campioni.
- wave.truncate() - taglia la forma d'onda dopo un numero di campioni.
- wave.zero_pad() - aggiunge alla fine una sequenza di zeri.
a = [23,34,45,56]
a[:3]
[23, 34, 45]
def zero_pad(array, n):
"""
Estende un Array con zeros.
array: numpy array
n: lunghezza finale
returns: new NumPy array
"""
res = np.zeros(n)
res[: len(array)] = array
return res
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
"""
Slitta a destra o sinistra nel tempo
shift: float time shift
"""
self.ts += shift
def roll(self, roll):
"""
Shifta di n campioni la forma d'onda (defasaggio)
"""
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
"""
Tronca la forma d'onda dopo n campioni
n: integer index
"""
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
"""
Stabilita una lunghezza in campioni aggiunge n zero alla fine
n: integer index
"""
self.ys = zero_pad(self.ys, n) # Richiama la funzione esterna
self.ts = self.start + np.arange(n) / self.framerate
a = pym.Sinusoid(1, 0.6, 0) # Istanza di Sinusoid (freq amp fase)
b = a.make_wave(a.period * 3) # Crea un'istanza di Wave - Durata in secondi
b.shift(a.period*0.25) # Secondi - Aggiunge del tempo (anche negativo)
a.plot() # Blu
b.plot() # Arancio
b = a.make_wave(a.period * 3)
b.roll(4000) # Campioni - non aggiunge del tempo (defasaggio)
a.plot() # Blu
b.plot() # Arancio
b = a.make_wave(a.period * 3)
b.truncate(6000) # Campioni
b.shift(0.3)
a.plot() # Blu
b.plot() # Arancio
b = a.make_wave(a.period * 3)
b.zero_pad(b.framerate*5) # Size finale dell'array (aggiunge zeri alla fine)
a.plot()
b.plot() # Arancio
Scrivere un soundfileIndice
Possiamo salvare un oggetto Wave sotto forma di sound file (in formato .wav).
- definiamo la funzione normalize che normalizza i valori ys a un ampiezza massima.
- definiamo la funzione quantize che quantizza (approssima) i valori ys al formato informatico utilizzato.
- definiamo la classe WavFileWriter che possiamo richiamare invocando il metodo write all'interno della classe Wave.
def normalize(ys, amp=1.0):
"""Normalizza i valori ys a +amp or -amp.
ys: wave array
amp: ampiezza massima alla quale normalizzare i valori
returns: wave array
"""
high, low = abs(max(ys)), abs(min(ys))
return amp * ys / max(high, low)
def quantize(ys, bound, dtype):
"""Maps the waveform to quanta.
ys: wave array
bound: maximum amplitude
dtype: numpy data type of the result
returns: segnale quantizzato
"""
if max(ys) > 1 or min(ys) < -1:
warnings.warn("Warning: devi normalizzare!")
ys = normalize(ys) # Se i valori eccedono +/-1 invoca la funzione normalizza
zs = (ys * bound).astype(dtype)
return zs
class WavFileWriter:
"""Scrive un file WAV."""
def __init__(self, filename="sound.wav", framerate=11025):
"""
filename: string
framerate: samples per second
"""
self.filename = filename
self.framerate = framerate
self.nchannels = 1
self.sampwidth = 2 # profondità di quantizzazione (bytes)
self.bits = self.sampwidth * 8 # numero di bits
self.bound = 2 ** (self.bits - 1) - 1 # Numero di livelli
self.fmt = "h" # formato
self.dtype = np.int16 # formato
self.fp = open_wave(self.filename, "w") # alias dalla libreria wave.open()
self.fp.setnchannels(self.nchannels)
self.fp.setsampwidth(self.sampwidth)
self.fp.setframerate(self.framerate)
def write(self, wave):
"""
wave: istanza di Wave
"""
zs = wave.quantize(self.bound, self.dtype) # Richiama la funzione quantize
self.fp.writeframes(zs.tobytes())
def close(self):
self.fp.close()
Aggiungiamo due metodi alla classe Wave.
- write() che richiama la classe WavFileWriter.
- normalize() che valuta la funzione corrispondente.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype): # Quantizza i valori al formato corretto
"""
Rounding dinamico
bound: ampiezza massima
dtype: numpy data type or string
returns: segnale quantizzato
"""
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
"""
amp: float ampiezza
"""
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"): # Proprietà come stringa
"""
Richima la classe WavFileWriter
"""
print("Writing", filename) # Monitor visivo
wfile = WavFileWriter(filename, self.framerate) # Richiama la classe
wfile.write(self) # Genera il file wav
wfile.close() # Lo chiude
a = pym.Sinusoid(1500, 1, 0) # Istanza di Sinusoid (freq amp fase)
b = a.make_wave(1) # Istanza di Wave - Durata in secondi
b.write('suoni/soundfile.wav') # Scrive il soundfile
Writing suoni/soundfile.wav
Ora possiamo leggere ed eseguire il soundfile con una qualsiasi DAW oppure direttamente dal codice.
Eseguire un soundfileIndice
Possiamo eseguire un soundfile dal codice in due modi:
- Aprendo da terminale il player di sistema (per MAC è afplay).
- Creando un oggetto Audio della libreria IPYthon.
Nel primo caso prima definiamo la funzione play_wave che valuteremo successivamente invocando un metodo specifico da aggiungere alla classe Wave.
Nel secondo caso scriviamo direttamente il metodo.
def play_wave(filename="sound.wav", player="afplay"):
"""Esegue un file wav.
filename: string
player: il nome della daw da utilizzare per eseguire il file
"""
cmd = "%s %s" % (player, filename) # comando da eseguire dalla shell (terminale)
popen = subprocess.Popen(cmd, shell=True)
popen.communicate()
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
"""
filename: string
"""
self.write(filename) # scrive il file
play_wave(filename) # valuta la funzione
def make_audio(self):
"""
Crea un oggetto Audio di IPython.
"""
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
a = pym.Sinusoid(500, 1, 0) # Istanza di Sinusoid (freq amp fase)
b = a.make_wave(1) # Istanza di Wave - Durata in secondi
b.play('suoni/soundfile.wav') # Legge con afplay
Writing suoni/soundfile.wav
b.make_audio() # Crea oggetto Audio di IPython
Importare un soundfileIndice
Possiamo generare automaticamente un'istanza di Wave importando un file .wav.
Definiamo la funzione read_wave che estrae i valori ys dal sound file grazie ad alcune funzionalità della libreria wave e li usa per generare un'istanza dell'oggetto Wave.
def read_wave(filename="sound.wav"):
"""
filename: string
returns: Wave
"""
fp = open_wave(filename, "r") # Dalla libreria wave
nchannels = fp.getnchannels()
nframes = fp.getnframes()
sampwidth = fp.getsampwidth()
framerate = fp.getframerate()
z_str = fp.readframes(nframes)
fp.close()
dtype_map = {1: np.int8, 2: np.int16, 3: "special", 4: np.int32} # Dict di formati informatici
if sampwidth not in dtype_map: # Se il formato non è riconosciuto
raise ValueError("formato %d sconosciuto" % sampwidth) # messaggio di errore
if sampwidth == 3: # Se è una stringa
xs = np.fromstring(z_str, dtype=np.int8).astype(np.int32) # la converte in int32
ys = (xs[2::3] * 256 + xs[1::3]) * 256 + xs[0::3]
else:
ys = np.frombuffer(z_str, dtype=dtype_map[sampwidth]) # altrimenti sceglie
# specificato
if nchannels == 2: # Se è stereo prende solo il
ys = ys[::2] # Primo canale
wave = Wave(ys, framerate=framerate) # ts è ricavato da ys in Wave
wave.normalize()
return wave
a = pym.read_wave('suoni/voce.wav') # genera un'istanza di Wave dal sound file
a.framerate
44100
a.plot(color="black",linewidth=1)
a.make_audio()
Estrarre un segmentoIndice
Quando generiamo un'istanza di wave da un sound file possiamo avere la necessità di estrarre un frammento e restituire una nuova istanza di Wave con il frammento selezionato.
Vediamo queli operazioni sono necessarie.
- stabilire un inizio e una durata del frammento da estrarre in secondi.
- definire un metodo per recuperare il valore degli indici dell'Array corrispondenti a inizio e fine.
- definire un metodo che realizzi uno slicing sull'Array ys.
- definire un metodo che generi una nuova istanza di Wave che contiene il frammento.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename) # scrive il file
play_wave(filename) # valuta la funzione
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
"""
Returns: una copia dell'istanza
"""
return copy.deepcopy(self)
def find_index(self, t):
"""
Calcola l'indice corrispondente
a un tempo dato in secondi
return: index int
"""
n = len(self) # numero di campioni
start = self.start # inizio in secondi
end = self.end # fine in secondi
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
"""
Estrae un frammento.
start: float inizio in secondi
duration: float durata in secondi
returns: Wave
"""
if start is None: # se non è specificato inizio vai all'indice 0
start = self.ts[0]
i = 0
else: # altrimenti calcola l'indice dell'inizio
i = self.find_index(start)
# calcola l'indice della fine
# (inizio + durata)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j) # valuta la funzione successiva...
def slice(self, i, j):
"""
Esegue uno slicing sugli Array di Wave
e genera una copia.
i: primo slice index
j: ultimo slice index
"""
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
a = pym.read_wave('suoni/voce.wav') # Genera un'istanza di Wave dal sound file
b = a.segment(2.2, 0.1) # Estrae un frammento e genera una nuova istanza di Wave
b.plot(color="red",linewidth=1)
b.make_audio()
Inviluppi d'ampiezzaIndice
In informatica musicale possiamo modificare l'ampiezza di un segnale principalmente in tre modi:
- riscalarla moltiplicando tutti i valori dei campioni (ys) per un valore costante compreso tra 0.0 e 1.0.
- definire un inviluppo d'ampiezza ovvero moltiplicare tutti i valori dei campioni (ys) per un valore che cambia nel tempo sempre compreso tra 0.0 e 1.0.
- definire una finestra di pochi campioni come inviluppo d'ampiezza attraverso una funzione (hanning. hamming, welch, etc.).
Come vedremo ognuna di queste modalità avrà una propria applicazione in contesti differenti.
Definiamo tre metodi all'interno della classe Wave.
- scale() - riscalaggio costante.
- window() - inviluppo d'ampiezza.
- hamming() - windowing per analisi e risintesi.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
"""
factor: fattore di riscalaggio (tra 0 e 1)
"""
self.ys *= factor # Moltiplica e aggiorna l'array
def window(self, window):
"""
window: sequenza di fattori di riscalaggio
della stessa lunghezza di self.ys
"""
self.ys *= window
def hamming(self):
"""
Applica una Hamming window al segnale.
"""
self.ys *= np.hamming(len(self.ys))
scale()Indice
a = pym.read_wave('suoni/voce.wav')
b = a.segment(2.2,0.1)
b.scale(0.3) # riscala
b.plot(color="red",linewidth=1)
b.make_audio()
window()Indice
Per questo medodo dobbiamo definire esternamente un'Array di valori della stessa lunghezza di ys.
a = pym.read_wave('suoni/voce.wav')
b = a.segment(2.2,0.5)
n = b.duration # Otteniamo la durata in secondi
t = len(b) # Otteniamo la capacità in campioni
print(n)
print(t)
0.5 22050
linen()
Definiamo una funzione per generare un inviluppo trapezoidale/triangolare.
Fadein e fadeout sono indicati sotto forma di lista e in tempo relativo, ovvero come fattori di moltiplicazione della durata totale.
def linen(duration=1, fade=[0.1,0.3], framerate=11025):
"""
duration: float durata totale in secondi
fade: float tempo di [fade in, fade out] somma <= 1.0
framerate:int rata di campionamento
returns: np.ndarray
"""
n = int(duration * framerate) # durata in frames
k1 = int(fade[0] * n) # tempo di fadein in frames
k2 = int(fade[1] * n) # tempo di fadeout in frames
w1 = np.linspace(0, 1, k1) # fade in
w2 = np.ones(n - (k1 + k2)) # sostegno
w3 = np.linspace(1, 0, k2) # fade out
window = np.concatenate((w1, w2, w3))
return window
e = pym.linen(0.5, [0.1,0.1], 44100)
plt.plot(e,'r:') # Plot
print(len(e)) # lunghezza in frames
22050
Passiamo la proprietà all'istanza di Wave invocando il metodo window().
a = pym.read_wave('suoni/voce.wav')
b = a.segment(2.2,0.4)
dur = b.duration # Otteniamo la durata in secondi
fade = [0.1,0.1]
rate = b.framerate # Otteniamo la framerate
e = pym.linen(dur, fade, rate)
b.window(e)
b.plot(color="red",linewidth=1)
b.make_audio()
fade()
Definiamo una versione di linen() dove possiamo specificare un solo tempo di fade in valori assoluti (secondi).
def fade(duration=1, fade=0.02, framerate=11025):
"""
duration: float durata totale in secondi
fade: float tempo del fade in secondi
framerate:int rata di campionamento
returns: np.ndarray
"""
n = int(duration * framerate) # durata in frames
k1 = int(fade * framerate) # tempo di fadein in frames
w1 = np.linspace(0, 1, k1) # fade in
w2 = np.ones(n - (k1 * 2)) # sostegno
w3 = np.linspace(1, 0, k1) # fade out
window = np.concatenate((w1, w2, w3))
return window
e = pym.fade(0.5, 0.02, 44100)
plt.plot(e,'r:') # Plot
print(len(e)) # lunghezza in frames
22050
a = pym.read_wave('suoni/voce.wav')
b = a.segment(3.4,0.1)
dur = b.duration # Otteniamo la durata in secondi
fad = 0.02
rate = b.framerate # Otteniamo la framerate
e = pym.fade(dur, fad, rate)
b.window(e)
b.plot(color="red",linewidth=1)
b.make_audio()
adsr()
Definiamo un'altra funzione che controlla un inviluppo di tipo ADSR dove passeremo le proprietà sotto forma di lista.
def adsr(duration=1, adsr=[0.1,0.1,0.5,0.5], framerate=11025):
"""
duration: float durata totale in secondi
adsr: list attacco, decadimento, sostegno, rilascio
framerate:int rata di campionamento
returns: np.ndarray
"""
n = int(duration * framerate) # durata in frames
a = int(adsr[0] * n) # attacco in frames
d = int(adsr[1] * n) # decadimento in frames
s = adsr[2] # livello di sostegno
r = int(adsr[3] * n) # release in frames
st = n - (a+d+r) # calcola il tempo di sostegno in frames
w1 = np.linspace(0, 1, a)
w2 = np.linspace(1, s, d)
w3 = np.ones(st) * s
w4 = np.linspace(s, 0, r)
window = np.concatenate((w1, w2, w3,w4))
return window
e = pym.adsr(0.5, [0.1,0.2,0.5,0.3], 44100)
plt.plot(e,'r:') # Plot
print(len(e)) # lunghezza in frames
22050
a = pym.read_wave('suoni/voce.wav')
b = a.segment(2.2,0.4)
dur = b.duration # Otteniamo la durata in secondi
env = [0.1, 0.1, 0.6, 0.6]
rate = b.framerate # Otteniamo la framerate
e = pym.adsr(dur, env, rate)
b.window(e)
b.plot(color="red",linewidth=1)
b.make_audio()
hamming()Indice
Quando vogliamo effettuare un'analisi spettrale di un suono abbiamo bisogno di applicare dei particolari tipi di inviluppo (window) generati da funzioni matematiche.
Per praticità ne abbiamo definito come metodo della classe Wave solo un tipo (Hamming window) che è quello che utilizzeremo nei paragrafi dedicati all'analisi del suono.
a = pym.read_wave('suoni/voce.wav')
b = a.segment(1.2,0.1)
b.hamming()
b.plot(color="red",linewidth=1)
b.make_audio()
Esercizi 1Indice
- Scaricare da freesound.org un soundfile.
- Selezionare un segmento di durata massima di 500ms.
- Applicare almeno tre inviluppi diversi che ne modifichino le caratteristiche percettive.
- Computare e visualizzare per ognuno la forma d'onda risultante.
- Salvare i segmenti in soundfiles.
- Scrivere una funzione chiamata stretch che prende una delle istanze di Wave risultanti e un fattore di streching attraverso il quale velocizzare o rallentare il suono agendo su ts e framerate.
- Aggiungere un metodo alla classe Wave per realizzare un reverse dei frammenti.
Secondo promemoria (dominio delle frequenze)Indice
Il timbro di un suono è definito principalmente dalla sua forma d'onda.
Possiamo analizzarlo attraverso diverse tecniche.
Una di queste basata sul teorema di Fourier lo scompone come somma di sinusoidi ognuna con una propria frequenza, una propria ampiezza e una propria fase.
Ogni singola sinusoide si chiama parziale.
La scomposizione avviene applicando una formula matematica chiamata Discrete Fourier Transform (DFT) che produce lo spettro di quel suono.
L'algoritmo che useremo per compiere questa operazione si chiama Fast Fourier Transform (FFT) che è un metodo efficente per computare la DFT.
SpettrogrammaIndice
Valutiamo il seguente codice che ci permette di visualizzare il risulatato dell'FFT in uno spettrogramma dove sull'asse delle x abbiamo la frequenza mentre sull'asse delle y l'ampiezza dei parziali.
N.B. Nei prossimi paragrafi entreremo nel merito, per ora utilizziamo in metodo wave.make_spectrum() come utilità.
def find_index(x, xs):
n = len(xs)
start = xs[0]
end = xs[-1]
i = round((n - 1) * (x - start) / (end - start))
return int(i)
class _Spectra(): # Classe Privata
"""Contiene codice comune a Spectrum e DTC"""
def __init__(self, hs, fs, framerate, full=False):
"""Inizializza uno spettro.
hs: array di ampiezze (reali o complesse)
fs: array of frequenze (bins)
framerate: frames per secondo
full: boolean per indicare full FFT o FFT reale
"""
self.hs = np.asanyarray(hs)
self.fs = np.asanyarray(fs)
self.framerate = framerate
self.full = full
@property
def max_freq(self): # Riporta la Frequenza di Nyquist
return self.framerate / 2
@property
def amps(self): # Riporta le ampiezze dei bins
return np.absolute(self.hs)
@property
def power(self): # Riporta le magnitudini
return self.amps ** 2
def render_full(self, high=None): # Estrae ampiezze e frequenze da un full spectrum
hs = np.fft.fftshift(self.hs)
amps = np.abs(hs)
fs = np.fft.fftshift(self.fs)
i = 0 if high is None else find_index(-high, fs)
j = None if high is None else find_index(high, fs) + 1
return fs[i:j], amps[i:j]
def plot(self, high=None,y_lim=[0,1],soglia=1,curva="linear",**kvargs): # High massima frequenza
if self.full: # y_lim limite di visualizzazione ampiezze
fs, amps = self.render_full(high) # soglia = per eliminare rumore di fondo
amps_id = amps > soglia # Array di 0 e 1
amps_clean = amps * amps_id # Taglia quelli sotto la soglia
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(fs, amps_clean, **kvargs)
else:
i = None if high is None else find_index(high, self.fs)
amps_id = self.amps > soglia
amps_clean = self.amps * amps_id
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.fs[:i], amps_clean[:i],**kvargs)
def plot_power(self, high=None,y_lim=[0,1],soglia=1,curva="linear",**kvargs):
if self.full:
fs, amps = self.render_full(high)
amps_id = amps > soglia
amps_clean = amps * amps_id
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(fs, amps_clean ** 2, **kvargs)
else:
i = None if high is None else find_index(high, self.fs)
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.fs[:i], self.power[:i],**kvargs)
class Spectrum(_Spectra): # Sottoclasse
"""Rappresenta lo spettro di un segnale"""
def __len__(self): # Numero di bins
return len(self.hs)
def scale(self, factor):
"""Moltiplica tutti gli elementi per un fattore
factor: fattore di moltiplicazione delle magnitudini (anche numeri complesso)
"""
self.hs *= factor
class Wave:
"""Rappresenta una forma d'onda generica discreta"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
"""
Calcola lo spettro da FFT
full = calcola la FFT intera e non la reale
returns: Spectrum
"""
n = len(self.ys) # numero di campioni
d = 1 / self.framerate # inverso della rata di campionamento = tempo tra i campioni (secondi)
if full:
hs = np.fft.fft(self.ys) # esegue la FFT
fs = np.fft.fftfreq(n, d) # restituisce un np.array di numeri complessi con magnitudini e fasi
else:
hs = np.fft.rfft(self.ys) # real FFT (su numeri reali e non complessi)
# restituisce un np.array di numeri reali
fs = np.fft.rfftfreq(n, d) # bins
# restituisce un np.array con le frequenze corrispondenti
return Spectrum(hs, fs, self.framerate, full)
a = pym.Sinusoid(300,1,0) # Genera un Array di campioni
b = a.make_wave(0.05) # Genera un'istanza di Wave
b.plot(color="blue",linewidth=1)
spettro = b.make_spectrum() # Computa lo spettro
spettro.scale(0.5) # Riscala l'ampiezza per un fattore di moltiploicazione (migliore visuale)
spettro.plot(y_lim=[0,150],color='red') # Visualizza il plot
b.make_audio()
Spettri fissiIndice
A seconda dei rapporti di frequenza che intercorrono tra i parziali possiamo classificare il timbro in due categorie:
- spettri armonici
- spettri inarmonici
Spettri armoniciIndice
Se le frequenze delle sinusoidi che compongono uno spettro hanno un rapporto tra numeri interi (1:3, 2:4, etc) possiamo definire quel suono armonico e il parziale più basso fondamentale.
Questo tipo di spettri sono generati sempre da forme d'onda periodiche.
Computiamo alcune forme d'onda classiche che hanno questa caratteristica.
Onda triangolareIndice
Ci sono molti modi per calcolare un'onda triangolare, vediamone uno definendo la classe TriangleSignal() figlia dalla classe Sinusoid eredita dunque le proprietà freq, amp, offset.
def unbias(ys): # Funzione che trasla un Array in modo che abbia come media 0.
return ys - ys.mean() # una sorta di remove DC offset
class TriangleSignal(Sinusoid):
"""Rappresenta un'onda triangolare bipolare"""
def evaluate(self, ts):
"""
ts: float array di onsets
returns: float array di ampiezze istantanee
"""
ts = np.asarray(ts) # Eventuale casting in np.ndarray
cycles = self.freq * ts + self.offset / PI2 # Numero di cicli dall'inizio
frac, _ = np.modf(cycles) # Splitta in ([parte decimale], [parte intera])
# prende solo i decimali (_ come variabile significa
# non prendere in considerazione)
# tra 0.0 e 1.0
ys = np.abs(frac - 0.5) # tra -0.5 e 0.5 (trasla di 0.5)
ys = normalize(unbias(ys), self.amp) # la riporta tra -amp e +amp
return ys
sig = pym.TriangleSignal(200,1,0)
sig.plot()
wave = sig.make_wave(0.5, 10000) # durata = 0.5 secondi, framerate = 10000
spek = wave.make_spectrum()
spek.plot(y_lim=[0,2600],color="red") # per zoomare mettere 600
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Come possiamo notare dallo spettrogramma sono presenti solo i parziali dispari (1:1,1:3,1:5, etc.) e il rapporto tra le ampiezze è strettamente legato alle frequenze:
a_parz = freq_fond / n_parz^2
fond = 200
print(fond / 1**2 / fond) # normalizzati...
print(fond / 3**2 / fond)
print(fond / 5**2 / fond)
print(fond / 7**2 / fond)
# ...
1.0 0.1111111111111111 0.04 0.020408163265306124
Possiamo chiamare questo rapporto anche struttura armonica.
Onda quadraIndice
Un'altra forma d'onda armonica classica degli albori della musica elettronica è l'onda quadra.
Definiamo la Classe SquareSignal() molto simile a TriangleSignal e anch'essa figlia di Sinusoid().
class SquareSignal(Sinusoid):
"""Rappresenta un'onda quadra bipolare"""
def evaluate(self, ts):
"""
ts: float array di onsets
returns: float array di ampiezze istantanee
"""
ts = np.asarray(ts)
cycles = self.freq * ts + self.offset / PI2
frac, _ = np.modf(cycles) # Solo parte decimale tra 0 e 1
ys = unbias(frac) # Bipolare
ys = self.amp * np.sign(ys) # np.sign() = valori negativi -> -1.0, valori positivi -> 1.0
return ys
sig = pym.SquareSignal(200,0.9,0)
sig.plot()
wave = sig.make_wave(0.5, 10000) # durata = 0.5 secondi, framerate = 10000
spek = wave.make_spectrum()
spek.plot(y_lim=[0,3000],soglia=100,color="red")
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Come possiamo notare dallo spettrogramma anche nell'onda quadra sono presenti solo i parziali dispari (1:1,1:3,1:5, etc.) ma il rapporto tra le ampiezze è diverso e si riducono con una curva più morbida (lineare):
a_parz = freq_fond / n_parz
fond = 200
print(fond / 1 / fond) # normalizzati...
print(fond / 3 / fond)
print(fond / 5 / fond)
print(fond / 7 / fond)
# ...
1.0 0.33333333333333337 0.2 0.14285714285714288
AliasingIndice
Analizziamo lo spettro di un'onda triangolare campionato con una framerate di 10.000 e la frequenza fondamentale a 1.300Hz.
sig = pym.TriangleSignal(1300)
wave = sig.make_wave(1, 10000)
spek = wave.make_spectrum()
spek.plot(y_lim=[0,800],soglia=50,color='red')
Possiamo osservare che, oltre ai primi due parziali a 1.300 e 3.900 Hz ce ne sono altri non previsti.
Queste si chiamano frequenze alias e sono generate dal fenomeno del foldover o aliasing dovuto alla perdita di informazioni che si verifica quando discretizziamo un segnale (non conosciamo i valori tra un campione e il successivo).
Prendiamo come ulteriore esempio due onde cosinusoidali entrambe con una framerate a 10.000 Hz.
La prima con una frequenza di 4.500 Hz
framerate = 10000
sig = pym.Sinusoid(4500,func=np.cos)
dur = sig.period*5
wave = sig.make_wave(dur, framerate=framerate)
wave.plot_vlines(color="red",linewidth=1,linestyle='dotted')
La Seconda con una frequenza di 5.500 Hz.
framerate = 10000
sig = pym.Sinusoid(5500,func=np.cos)
dur = sig.period*6
wave = sig.make_wave(dur, framerate=framerate)
wave.plot_vlines(color="red",linewidth=1,linestyle='dotted')
Osserviamo che sono identiche perchè quando campioniamo un segnale con una frequenza di 5.500 Hz a 10.000 campioni per secondo il risultato non è distiguibile dal campionamento di un segnale a 5.500 Hz.
Per ovviare a questo problema secondo il teorema di Nyquist-Shannon dobbiamo scegliere una rata di campionamento (framerate) che sia almeno il doppio della frequenza del parziale più acuto presente nello spettro ottenendo così un minimo di due campioni per ciclo.
Le più comuni frequenze di campionamento audio standard sono 44.100, 48.000, 96.000 e loro multipli.
class SumSignal(Signal):
"""Rappresenta la somma di segnali."""
def __init__(self, *args):
"""
args: tuple di signals
"""
self.signals = args
def evaluate(self, ts):
"""
ts: float array of times
returns: float wave array
"""
ts = np.asarray(ts)
return sum(sig.evaluate(ts) for sig in self.signals)
sig = pym.Sinusoid(10,0.6) + pym.Sinusoid(20,0.2) + pym.Sinusoid(40,0.1) + pym.Sinusoid(80,0.2) # Somma
sig.plot()
sig = pym.Sinusoid(100,0.6) + pym.Sinusoid(200,0.2) + pym.Sinusoid(400,0.1) + pym.Sinusoid(800,0.05) # Somma
wave = sig.make_wave(1, 11025)
spek = wave.make_spectrum()
spek.plot(high=900,y_lim=[0,3500],soglia=1,color='red')
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Questa tecnica funziona solamente con spettri armonici in quanto la durata di un ciclo deve essere la stessa per tutti i parziali.
Possiamo anche sommare tra loro forme d'onda diverse (tenendo conto dell'aliasing).
sig = pym.TriangleSignal(20,0.1) + pym.SquareSignal(30,0.1)
sig.plot()
sig = pym.TriangleSignal(100,0.1) + pym.SquareSignal(200,0.1)
wave = sig.make_wave(1, 44100)
spek = wave.make_spectrum()
spek.plot(high=900,y_lim=[0,1200],soglia=1,color='red')
sig = pym.TriangleSignal(100,0.1) + pym.SquareSignal(200,0.1) + pym.Sinusoid(800,0.3)
wave = sig.make_wave(1, 44100)
dur = wave.duration # Otteniamo la durata in secondi
fad = [0.1,0.2,0.5,0.3] # Definiamo i parametri
rate = wave.framerate # Otteniamo la framerate
env = pym.adsr(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Spettri inarmoniciIndice
Se vogliamo realizzare la sintesi additiva di spettri inarmonici dobbiamo cambiare strategia di programmazione e sommare tra loro non forma d'onda (Signals) ma onde (waves).
Per farlo agggiungiamo un metodo dedicato alla classe wave.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def __add__(self, other):
"""Somma due wave campione per campione.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate # verifica che le framerate siano uguali
# genera un array di tempi che copre entrambe le waves
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n) # Array di zero
ts = start + np.arange(n) / self.framerate # Array di tempi
def add_ys(wave): # Somma i valori dei campioni
i = find_index(wave.start, ts)
# si assicura che non ci siano 'salti' (discontinuità) tra i tempi
diff = ts[i] - wave.start
dt = 1 / wave.framerate # tempi delta tra campioni
if (diff / dt) > 0.1:
warnings.warn(
"Non posso sommare; il loro " "tempo non coincide."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor # Moltiplica e aggiorna l'array
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
n = len(self.ys) # numero di campioni
d = 1 / self.framerate # inverso della rata di campionamento = tempo tra i campioni (secondi)
if full:
hs = np.fft.fft(self.ys) # esegue la FFT
fs = np.fft.fftfreq(n, d)
else:
hs = np.fft.rfft(self.ys) # real FFT (su numeri reali e non complessi)
# restituisce un np.array di numeri complessi con magnitudini e fasi
fs = np.fft.rfftfreq(n, d) # bins
# restituisce un np.array con le frequenze corrispondenti
return Spectrum(hs, fs, self.framerate, full)
mix = pym.Sinusoid(10,0.2).make_wave(0.5,11025) + pym.Sinusoid(11,0.2).make_wave(0.5,11025) + pym.Sinusoid(13,0.2).make_wave(0.5,11025)
mix.plot()
dur_a = 0.2
sig_a = pym.Sinusoid(800,0.3).make_wave(dur_a,11025)
env_a = pym.adsr(dur_a, [0.1,0.2,0.5,0.3], 11025)
sig_a.window(env_a)
dur_b = 1.2
sig_b = pym.Sinusoid(820,0.3).make_wave(dur_b,11025)
env_b = pym.adsr(dur_b, [0.1,0.2,0.5,0.3], 11025)
sig_b.window(env_b)
dur_c = 1.6
sig_c = pym.Sinusoid(987,0.3).make_wave(dur_c,11025)
env_c = pym.adsr(dur_c, [0.1,0.2,0.5,0.3], 11025)
sig_c.window(env_c)
wave = sig_a + sig_b + sig_c
wave.make_audio()
Esercizi 2Indice
- Disegnare una forma d'onda complessa attraverso la somma di forme d'onda complesse (sintesi additiva a spettro fisso).
- Non ci devono essere discontinuità tra inizio e fine del ciclo.
- Generare un suono con:
- una propria frequenza.
- una propria durata.
- un proprio inviluppo d'ampiezza.
- Computare e salvare un sound file.
- Computare e visualizzare la forma d'onda risultante.
- Computare e visualizzare lo spettro risultante.
- Disegnare una forma d'onda complessa attraverso la somma di forme d'onda complesse (sintesi additiva a spettro fisso).
- Realizzare un suono complesso attraverso la somma di sinusoidi ognuna con:
- una propria frequenza
- una propria durata (N.B. gli array per essere sommati devono avere tutti lo stesso size...)
- una propria fase.
- un proprio inviluppo d'ampiezza
- Computare e salvare un sound file.
- Computare e visualizzare la forma d'onda risultante.
- Computare e visualizzare lo spettro risultante.
- Realizzare un suono complesso attraverso la somma di sinusoidi ognuna con:
- Definire una classe SawToothSignal che estende Signal allo stesso modo di TriangleSignal e SquareSignal.
- Computare e visualizzare lo spettro risultante e descriverne le caratteristiche.
- Definire un'onda quadra con una frequenza di 1100 Hz e realizzare un'istanza di Wave con una frequenza di campionamento di 10.000 fps.
- Computare e visualizzare lo spettro risultante.
- C'è aliasing? ed eventualmente quali sono le frequenze introdotte?.
Spettri variabiliIndice
Gli spettri appena illustrati sono fissi ovvero le frequenze e le ampiezze dei singoli parziali non variano nel tempo.
L'eventuale inviluppo di ampiezza è identico per tutti i parziali:
I suoni presenti in natura hanno però spettri variabili.
Ogni singolo parziale segue un proprio percorso sia per quanto riguarda l'ampiezza che la frequenza ( microglissati ).
La sovrapposizione di questi percorsi si chiama inviluppo spettrale.
Isoliamo questi due fenomeni e analizziamone le caratteristiche.
Chirp lineareIndice
Generiamo un chirp lineare ovvero un segnale sinusoidale che glissa linearmente tra due frequenze (rampa lineare).
Vediamo come calcolare tutti i valori di ampiezza istantanea.
Cominciamo con ottenere un Array di frames (in secondi).
framerate = 1000
nf = np.arange(0,20,1) # Genera gli indici dei frames
ts = nf / framerate # Array di frames
print(nf)
print(ts)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19] [0. 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01 0.011 0.012 0.013 0.014 0.015 0.016 0.017 0.018 0.019]
Generiamo:
- un Array di frequenze interpolate tra inizio e fine.
- un Array di tempi delta tra i frames (essendo equispaziati è sempre lo stesso valore)
inizio = 220
fine = 880
freqs = np.linspace(inizio, fine, len(ts)-1) # Array di frequenze interpolate
dts = np.diff(ts) # Array di tempi delta (calcola il delta tra elementi adiacenti)
print(freqs)
print(dts)
[220. 256.66666667 293.33333333 330. 366.66666667 403.33333333 440. 476.66666667 513.33333333 550. 586.66666667 623.33333333 660. 696.66666667 733.33333333 770. 806.66666667 843.33333333 880. ] [0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001]
Se la frequenza è costante sappiamo che la fase si calcola con:
$ \phi = 2 \pi ft$
Se invece varia nel tempo come in un glissato dobbiamo calcolare di quanto cambia ad ogni intervallo.
$ \phi = 2 \pi f(t) \Delta t$
dfasi = PI2 * freqs * dts # Calcola i cambi di fase
print(dfasi)
[1.38230077 1.61268423 1.84306769 2.07345115 2.30383461 2.53421807 2.76460154 2.994985 3.22536846 3.45575192 3.68613538 3.91651884 4.1469023 4.37728576 4.60766923 4.83805269 5.06843615 5.29881961 5.52920307]
Calcoliamo tutte le fasi ad ogni istante sommando i nuovi valori ai precedenti.
Shiftiamo l'array di 1 elemento.
Inseriamo nell'array il valore della fase iniziale (0).
dfasi = np.roll(dfasi, 1) # Shifta le fasi di 1 elemento
fasi = np.cumsum(dfasi) # Calcola le fasi
fasi = np.insert(fasi, 0, 0) # Aggiunge il valore iniziale
print(fasi)
[ 0. 5.52920307 6.91150384 8.52418807 10.36725576 12.44070691 14.74454152 17.27875959 20.04336113 23.03834613 26.26371458 29.7194665 33.40560188 37.32212072 41.46902303 45.84630879 50.45397802 55.2920307 60.36046685 65.65928646]
Calcoliamo le ampiezze istantanee come funzione delle fasi (matematicamente la frequenza è una derivata della fase).
amp = 1 # Ampiezza di picco
ys = amp * np.sin(fasi) # Calcola le ampiezze istantanee
print(ys)
[ 0. -0.68454711 0.58778525 0.78369346 -0.80901699 -0.12533323 0.82114921 -1. 0.92977649 -0.8660254 0.90482705 -0.9921147 0.91354546 -0.36812455 -0.58778525 0.9573195 0.18738131 -0.95105652 -0.62114778 0.30901699]
Formalizziamo il tutto in una classe.
class Chirp(Signal):
"""Rappresenta un segnale con frequanza variabile - rampa lineare"""
def __init__(self, inizio=440, fine=880, amp=1.0):
""""
inizio: float frequenza in Hz
fine: float frequenza in Hz
amp: float ampiezza di picco
"""
self.inizio = inizio
self.fine = fine
self.amp = amp
@property
def period(self): # Restituisce il periodo del segnale in secondi.
return ValueError("Segnale non periodico")
def evaluate(self, ts): # Calcola le ampiezze a onsets equispaziati
"""
ts: float array di onsets
returns: float wave array
"""
freqs = np.linspace(self.inizio, self.fine, len(ts)-1) # Array di n frequenze
dts = np.diff(ts) # Calcola il tempo delta tra campioni
dfasi = PI2 * freqs * dts # Calcola i cambi di fase
dfasi = np.roll(dfasi, 1) # Shifta le fasi di 1
fasi = np.cumsum(dfasi) # Calcola la fase ad ogni campione
fasi = np.insert(fasi, 0, 0) # Aggiunge la prima fase
ys = self.amp * np.sin(fasi) # Calcola le ampiezze istantanee
return ys
sig = pym.Chirp(inizio=220,fine=880)
wave = sig.make_wave(duration=0.03)
wave.plot(color="red",linewidth=1)
sig = pym.Chirp(inizio=220,fine=880)
wave = sig.make_wave(3, 44100)
dur = wave.duration # Otteniamo la durata in secondi
fad = [0.1,0,1,0.1] # Definiamo i parametri
rate = wave.framerate # Otteniamo la framerate
env = pym.adsr(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Chirp esponenzialeIndice
L'orecchio umano percepisce le frequenze in modo logaritmico e non lineare. Se vogliamo che il glissato sia percepito in modo lineare dobbiamo realizzarlo come esponenziale.
Definiamo una nuova classe modificando leggermente la precedente.
class ExpoChirp(Signal):
"""Rappresenta un segnale con frequanza variabile - rampa esponenziale"""
def __init__(self, inizio=440, fine=880, amp=1.0):
""""
inizio: float frequenza in Hz
fine: float frequenza in Hz
amp: float ampiezza di picco
"""
self.inizio = inizio
self.fine = fine
self.amp = amp
@property
def period(self):
return ValueError("Segnale non periodico")
def evaluate(self, ts):
"""
ts: float array di onsets
returns: float wave array
"""
inizio, fine = np.log10(self.inizio), np.log10(self.fine) # Logaritmico
freqs = np.logspace(inizio, fine, len(ts)-1) # Logaritmico
dts = np.diff(ts)
dfasi = PI2 * freqs * dts
dfasi = np.roll(dfasi, 1)
fasi = np.cumsum(dfasi)
fasi = np.insert(fasi, 0, 0)
ys = self.amp * np.sin(fasi)
return ys
sig = pym.ExpoChirp(inizio=220,fine=880)
wave = sig.make_wave(3, 44100)
dur = wave.duration # Otteniamo la durata in secondi
fad = [0.1,0,1,0.1] # Definiamo i parametri
rate = wave.framerate # Otteniamo la framerate
env = pym.adsr(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
SonogrammaIndice
Per analizzare e visualizzare segnali che variano dinamicamente nel tempo come gli inviluppi spettrali lo spettrogramma che abbiamo utilizzato per le forma d'onda a spettro fisso non è il metodo migliore.
Come esempio computiamo lo spettrogramma di un chirp lineare.
sig = pym.Chirp(inizio=220,fine=440)
wave = sig.make_wave(1, 10000)
spek = wave.make_spectrum()
spek.plot(high=700,y_lim=[0,450],soglia=1,color="red",linewidth=1)
Informazioni ricavate dallo spettrogramma:
Le frequenze tra 220 e 440 Hz sono tutte presenti con la stessa ampiezza.
Il segnale occupa lo stesso tempo per tutte le frequenze.
Proviamo con il chirp esponenziale. Le frequenze più basse hanno maggiore ampiezza in quanto occupano più tempo.
Nessuna informazione riguardo il rapporto tra frequenza e tempo ( il glissato ).
Per ottenre questo tipo di informazione dobbiamo suddividere il glissato in segmenti e computare lo spettro di ognuno.
Il risultato è una Short-Time Fourier Trasform (STFT).
Ci sono molti modi di visualizzare una STFT, il più comune è un sonogramma dove:
- asse delle x - tempo,
- asse delle y - frequenza
- colore o toni di grigio - ampiezze.
Prima di procedere osserviamo alcuni parametri e problemtaiche condivise con gli spettrogrammi
Window size e limite di GaborIndice
Un parametro fondamentale della STFT è il window size ovvero da quanti punti (campioni) è formata la finestra di analisi (il singolo frammento).
I size più comuni sono 512, 1024, 2048, 4096 o 8192 e comunque multipli di due.
Size piccoli danno una maggiore risoluzione temporale.
Size grandi danno una maggiore risoluzione frequenziale .
Vediamo il perchè.
La risoluzione temporale è data dal rapporto tra window size e rata di campionamento ed è espressa in secondi.
rt = ws / sr
ws = 512
sr = 11025
rt = ws/sr
print(rt)
0.046439909297052155
La risoluzione frequenziale è data dal rapporto inverso.
rf = $ {sr/2 \over ws/2}$ = sr/ws
Ad esempio se il window size è di 512 campioni e la rata di campionamento di 11.025 Hz dividiamo lo spettro in 256 frequenze o bins (ws/2) in un range compreso tra 0 e 5512.5 Hz (sr/2).
ws = 512
sr = 11025
rf = sr / ws
print(rf)
21.533203125
Il range tra i bins è di 21.53Hz per 256 punti.
freqs = np.linspace(0, 5512.5, 256)
print(freqs)
[ 0. 21.61764706 43.23529412 64.85294118 86.47058824 108.08823529 129.70588235 151.32352941 172.94117647 194.55882353 216.17647059 237.79411765 259.41176471 281.02941176 302.64705882 324.26470588 345.88235294 367.5 389.11764706 410.73529412 432.35294118 453.97058824 475.58823529 497.20588235 518.82352941 540.44117647 562.05882353 583.67647059 605.29411765 626.91176471 648.52941176 670.14705882 691.76470588 713.38235294 735. 756.61764706 778.23529412 799.85294118 821.47058824 843.08823529 864.70588235 886.32352941 907.94117647 929.55882353 951.17647059 972.79411765 994.41176471 1016.02941176 1037.64705882 1059.26470588 1080.88235294 1102.5 1124.11764706 1145.73529412 1167.35294118 1188.97058824 1210.58823529 1232.20588235 1253.82352941 1275.44117647 1297.05882353 1318.67647059 1340.29411765 1361.91176471 1383.52941176 1405.14705882 1426.76470588 1448.38235294 1470. 1491.61764706 1513.23529412 1534.85294118 1556.47058824 1578.08823529 1599.70588235 1621.32352941 1642.94117647 1664.55882353 1686.17647059 1707.79411765 1729.41176471 1751.02941176 1772.64705882 1794.26470588 1815.88235294 1837.5 1859.11764706 1880.73529412 1902.35294118 1923.97058824 1945.58823529 1967.20588235 1988.82352941 2010.44117647 2032.05882353 2053.67647059 2075.29411765 2096.91176471 2118.52941176 2140.14705882 2161.76470588 2183.38235294 2205. 2226.61764706 2248.23529412 2269.85294118 2291.47058824 2313.08823529 2334.70588235 2356.32352941 2377.94117647 2399.55882353 2421.17647059 2442.79411765 2464.41176471 2486.02941176 2507.64705882 2529.26470588 2550.88235294 2572.5 2594.11764706 2615.73529412 2637.35294118 2658.97058824 2680.58823529 2702.20588235 2723.82352941 2745.44117647 2767.05882353 2788.67647059 2810.29411765 2831.91176471 2853.52941176 2875.14705882 2896.76470588 2918.38235294 2940. 2961.61764706 2983.23529412 3004.85294118 3026.47058824 3048.08823529 3069.70588235 3091.32352941 3112.94117647 3134.55882353 3156.17647059 3177.79411765 3199.41176471 3221.02941176 3242.64705882 3264.26470588 3285.88235294 3307.5 3329.11764706 3350.73529412 3372.35294118 3393.97058824 3415.58823529 3437.20588235 3458.82352941 3480.44117647 3502.05882353 3523.67647059 3545.29411765 3566.91176471 3588.52941176 3610.14705882 3631.76470588 3653.38235294 3675. 3696.61764706 3718.23529412 3739.85294118 3761.47058824 3783.08823529 3804.70588235 3826.32352941 3847.94117647 3869.55882353 3891.17647059 3912.79411765 3934.41176471 3956.02941176 3977.64705882 3999.26470588 4020.88235294 4042.5 4064.11764706 4085.73529412 4107.35294118 4128.97058824 4150.58823529 4172.20588235 4193.82352941 4215.44117647 4237.05882353 4258.67647059 4280.29411765 4301.91176471 4323.52941176 4345.14705882 4366.76470588 4388.38235294 4410. 4431.61764706 4453.23529412 4474.85294118 4496.47058824 4518.08823529 4539.70588235 4561.32352941 4582.94117647 4604.55882353 4626.17647059 4647.79411765 4669.41176471 4691.02941176 4712.64705882 4734.26470588 4755.88235294 4777.5 4799.11764706 4820.73529412 4842.35294118 4863.97058824 4885.58823529 4907.20588235 4928.82352941 4950.44117647 4972.05882353 4993.67647059 5015.29411765 5036.91176471 5058.52941176 5080.14705882 5101.76470588 5123.38235294 5145. 5166.61764706 5188.23529412 5209.85294118 5231.47058824 5253.08823529 5274.70588235 5296.32352941 5317.94117647 5339.55882353 5361.17647059 5382.79411765 5404.41176471 5426.02941176 5447.64705882 5469.26470588 5490.88235294 5512.5 ]
Queste due risoluzioni sono strettamante collegate in quanto all'aumentare dell'una diminuisce l'altra.
Questa limitazione è chiamata il limite di Gabor.
Leakage e windowingIndice
La DFT (Discrete Fourier Transform) parte dal presupposto che il segnale da analizzare sia periodico e che la finestra di analisi contenga un periodo o suoi multipli ovvero che non ci siano discontinuità alle estremità rendendolo idealmente infinito.
a = pym.Sinusoid(440) # Un periodo
b = a.make_wave(a.period * 30) # Trenta periodi
c = b.make_spectrum() # DFT
c.plot(high=880,y_lim=[0,400],soglia=1,color="red",linewidth=1) # Visualizzazione
Nella maggior parte dei casi però non è così e ci sono discontinuità del segnale ai lati della finestra.
a = pym.Sinusoid(440) # Un periodi
b = a.make_wave(a.period * 30.25) # 30.25 periodi
c = b.make_spectrum() # DFT
c.plot(high=880,y_lim=[0,400],soglia=1,color="red",linewidth=1) # Visualizzazione
Osserviamo come l'energia nello spettro sia distribuita anche in altre frequenze (tra 240 e 640 Hz circa).
Questa distribuzione si chiama dispersione spettrale (spectral leakage).
Per ovviare a questa problematica applichiamo un inviluppo d'ampiezza alla finestra smussando le discontinuità trasformando il segnale originale in modo funzionale all'analisi.
Possiamo utilizzare diverse funzioni per generare l'inviluppo, le principali sono hamming, hanning, barlett, blackman e kaiser tutte definibili in NumPy.
a = pym.Sinusoid(440) # Un periodi
b = a.make_wave(a.period * 10.25) # 10.25 periodi
s = b.ys # Ampiezze istantanee
w = np.hanning(len(s)) # Window
plt.plot(s)
plt.plot(w)
plt.plot(s*w)
[<matplotlib.lines.Line2D at 0x1525d8190>]
Hamming è quella più adatta a propositi generali e l'abbiamo inclusa come metodo della classe Wave.
Il tipo di inviluppo scelto può modificare in modo importante il risultato dell'analisi.
a = pym.Sinusoid(440) # Un periodi
b = a.make_wave(a.period*30.25) # 30.25 periodi
b.hamming() # Windowing
c = b.make_spectrum() # DFT
c.plot(high=880,y_lim=[0,400],soglia=1,color="red",linewidth=1) # Visualizzazione
Notiamo che il leakage è attenuato ma l'energia è dimezzata a causa del windowing.
make_spectrogram()Indice
Un sonogramma è una sequenza di spettrogrammi.
Per definirlo dobbiamo stabilire:
- il window size di ognuno.
- un fattore di overlap.
Definiamo prima la classe Sonogram che accetta due parametri:
- spec_map - un dictionary con (onsets : spettrogrammi).
- wsize - il size di ogni singolo spettrogramma.
class Sonogram:
"""Rappresenta un Sonogramma"""
def __init__(self, spec_map, wsize):
"""Inizializza.
spec_map: mappa da tempo (float) a spettro
wsize: window size di ogni frammento
"""
self.spec_map = spec_map
self.wsize = wsize
def any_spectrum(self):
"""Ogni singolo spettrogramma (vuoto)."""
index = next(iter(self.spec_map)) # Iteratore
return self.spec_map[index] # Richiama uno spettro alla volta compreso nel dictionary
@property
def time_res(self):
"""Risoluzione temporale in secondi"""
spectrum = self.any_spectrum()
return float(self.wsize) / spectrum.framerate
@property
def freq_res(self):
"""Risoluzione frequenziale in Hz."""
return self.any_spectrum().freq_res
def times(self): # Array di onsets
"""Sequenza di onsets ordinati in modo crescente (Sorted) in secondi.
"""
ts = sorted(iter(self.spec_map))
return ts
def frequencies(self): # Array di frequenze
"""Sequenza di frequenze (in Hz).
"""
fs = self.any_spectrum().fs # Richiama .fs sui singoli spettri
return fs
def plot(self, high=None):
"""Crea un Plot con pseudocolori.
high: la frequenza più alta da visualizzare
"""
fs = self.frequencies()
i = None if high is None else find_index(high, fs) # Possiamo specificare la frequenza massima
fs = fs[:i] # Slicing Array frequenze
ts = self.times() # Array tempi
size = len(fs), len(ts) # Size di entrambe gli array
array = np.zeros(size, dtype=float) # Genera un Array di zero
for j, t in enumerate(ts):
spectrum = self.spec_map[t] # Itera gli spettri dal dictionary
array[:, j] = spectrum.amps[:i] # Recupera le ampiezze di ogni spettro e le
# assegna a un array
plt.pcolormesh(ts, fs, array) # Visualizzazione onsets, frequenze, colori
Aggiungiamo alla classe Wave il metodo make_sonogram() che computa un sonogramma.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def __add__(self, other):
"""Somma due wave campione per campione.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n)
ts = start + np.arange(n) / self.framerate
def add_ys(wave):
i = find_index(wave.start, ts)
diff = ts[i] - wave.start
dt = 1 / wave.framerate
if (diff / dt) > 0.1:
warnings.warn(
"Non posso sommare; il loro " "tempo non coincide."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
n = len(self.ys)
d = 1 / self.framerate
if full:
hs = np.fft.fft(self.ys)
fs = np.fft.fftfreq(n, d)
else:
hs = np.fft.rfft(self.ys)
fs = np.fft.rfftfreq(n, d)
return Spectrum(hs, fs, self.framerate, full)
def make_sonogram(self, wsize, win_flag=True):
"""Calcola il sonogramma.
seg_length: window size
win_flag: boolean se applicare o meno il windowing con Hamming
returns: Spectrogram
"""
if win_flag: # Se True
window = np.hamming(wsize) # applica il windownig
i, j = 0, wsize # Variabili
step = int(wsize // 2) # Divide e approssima all'int più basso (fattore di overlap)
spec_map = {} # Crea un Dictionary vuoto (onset:spettro)
while j < len(self.ys):
segment = self.slice(i, j) # Slicing window dopo window
if win_flag: # Se True
segment.window(window) # Segmenta e applica hamming
t = (segment.start + segment.end) / 2 # Calcola la metà del segmento e la assegna a t (onset)
spec_map[t] = segment.make_spectrum() # Computa spettro corrente e lo inserisce nel dictionary
# uno Spectrogram per finestra
i += step # Incrementa inizio frammento
j += step # Incrementa fine frammento
return Sonogram(spec_map, wsize)
sig = pym.Chirp(inizio=220,fine=440)
wave = sig.make_wave(1, 11025)
spek = wave.make_sonogram(wsize=512)
spek.plot(high=780)
Esercizi 3Indice
- Scrivere una classe SawToothChirp che estende Chirp e sovrascrive evaluate per generare un onda a dente di sega la cui frequenza aumenta o diminuisce linearmente.
- Computare e visualizzare uno spettrogramma.
- Caricare un soundfile contenente una voce parlata.
- Computare e visualizzare uno spettrogramma.
- Siete in grado di identificare le vocali?.
NoiseIndice
Nell'ambito del signal processing il termine rumore è riferito a un segnale con una elevata componente spettrale che non può essere ricondotta alla struttura dei segnali periodici.
Principalmente hanno tutti a che fare con una generazione non-deterministica (random) dei valori di ampiezza istantanea.
Questo tipo di generazione dipende principalmente da tre caratteristiche.
Distribuzione
La distribuzione definisce la probabilità che esca un determinato valore in un determinato ambito.
Un esempio è dato dal rumore bianco che è caratterizzzato da una distribuzione lineare in quanto tutti i valori compresi tra +1 e -1 hanno la stessa probabilità di essere generati.
Un altro esempio è il rumore gaussiano i cui valori sono compresi tra -inf e +inf e le probabilità che siano generati valori attorno allo zero sono più alte rispetto a valori più lontani secondo la curva a campana gaussiana.
Correlazione
L'esistenza o meno di una relazione matematica di qualche tipo tra i diversi valori.
Nel rumore bianco ad esempio non c'è correlazione in quanto tutti i valori sono indipendenti.
Nel rumore browniano invece ogni nuovo valore è calcolato sommando al valore precedente uno step random.
La sequenza di valori è conosciuta anche come (random walk].
Energia vs frequenza
Nel rumore bianco l'energia è distribuita egualmente lungo tutto lo spettro e dunque tutte le frequenze hanno la stessa ampiezza media.
Nel rumore rosa invece l'energia è inversamente proporzonale alla frequenza.
L'ampiezza media a una frequenza $f$ è calcolabile secondo la formula $1/f$.
White noiseIndice
Rumore bianco che possiamo definire anche come rumore uniforme non correlato.
Uniforme sia perchè i valori di ampiezza istantanea seguono una distribuzione randomica uniforme sia perchè i parziali hanno tutti la stessa energia (ampiezza) lungo tutto lo spettro.
Non correlato perchè i valori di ampiezza istantanea sono indipendenti l'uno con l'altro ovvero se conosciamo un valore non possiamo ricavare alcuna informazione sugli altri.
Definiamo una sottoclasse privata di Signal come contenitore per la generazione dei diversi tipi di rumore.
class _Noise(Signal):
"""Rappresenta un segnale noise"""
def __init__(self, amp=1.0): # Ampiezza
self.amp = amp
@property
def periodo(self): # Periodo in secondi
return ValueError("Non-periodic signal.")
Definiamo un'altra sottoclasse per la generazione di rumore bianco esatamente come abbiamo fatto per le forme d'onda classiche.
class WhiteNoise(_Noise):
"""Rappresenta un rumore bianco"""
def evaluate(self, ts):
"""
ts: float array di tempi delta
returns: float array di ampiezze istantanee
"""
ys = np.random.uniform(-self.amp, self.amp, len(ts))
return ys
Forma d'onda.
sig = pym.WhiteNoise(amp=0.7)
sig.plot()
Spettro
Utilizziamo plot_power perchè nella visualizzazione del rumore è più convenzionale.
wave = sig.make_wave(0.5, 11025) # durata = 0.5 secondi, framerate = 11025
spek = wave.make_spectrum()
spek.plot_power(y_lim=[0,8000],color="red",linewidth=0.5) # plot_power
Applichiamo un inviluppo d'ampiezza anche se per il rumore è superfluo e generiamo un soundfile.
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Spettrogramma integraleIndice
Per visualizzare meglio le relazioni che intercorrono tra energia e frequenza di un noise possiamo realizzare uno spettrogramma integrale.
Basta calcolare i valori integrali delle ampiezze (energia cumulativa).
Definiamo la classe IntegratedSpectrum che potremo richiamare attraverso un nuovo metodo di Spectrum (make_integrated_spectrum()).
class IntegratedSpectrum:
"""Rappresenta l'integrale di uno spettro"""
def __init__(self, cs, fs):
"""
cs: sequenza di ampiezze cumulative
fs: sequenza di frequenze
"""
self.cs = np.asanyarray(cs)
self.fs = np.asanyarray(fs)
def plot_power(self, low=0, high=None, expo=False,**options):
"""
low: int indice da dove iniziare
high: int indice dove terminare
expo: lineare o esponenziale
"""
cs = self.cs[low:high]
fs = self.fs[low:high]
if expo:
cs = np.exp(cs)
plt.plot(fs, cs,**options)
class Spectrum(_Spectra): # Sottoclasse
"""Rappresenta lo spettro di un segnale"""
def __len__(self): # Numero di bins
return len(self.hs)
def scale(self, factor):
self.hs *= factor
def make_integrated_spectrum(self):
"""Genera il plot dello spettro integrale.
"""
cs = np.cumsum(self.power) # Somma cumulativa delle ampiezze (power ereditato da _Spectra())
cs /= cs[-1] # Divide per l'ultimo elemento riscalando tra 0 e 1
return IntegratedSpectrum(cs, self.fs)
sig = pym.WhiteNoise(amp=0.7)
wave = sig.make_wave(0.5, 11025)
spek = wave.make_spectrum() # Genera spettrogramma
inte = spek.make_integrated_spectrum() # Genera spettrogramma integrale da spettrogramma
inte.plot_power(color="red",linewidth=1,alpha=0.5) # plot_power
Da questo tipo di spettrogramma del rumore bianco possiamo notare come l'ampiezza media è costante a tutte le frequenze.
Brownian noiseIndice
Rumore browniano (rumore rosso) che possiamo definire anche come rumore non uniforme correlato.
E'chiamato così per analogia con il moto browniano nel quale le particelle di un fluido si muovono in modo apparentemente casuale dovuto a interazioni nascoste.
Questo tipo di moto può essere descritto da un modello matematico chiamato random walk.
In un random walk mono-dimensionale i valori aumentano o diminuiscono nel tempo sommando al valore precedente un passo randomico.
Il valore di qualsiasi punto nel tempo è la somma di tutti i passi precedenti.
Definiamo una classe figlia di _Noise.
class BrownianNoise(_Noise):
"""Rappresenta rumore browniano, aka rumore rosso."""
def evaluate(self, ts):
"""
ts: float array of times
returns: float wave array
"""
dys = np.random.uniform(-1, 1, len(ts)) # rumore bianco (non correlato)
ys = np.cumsum(dys) # somma cumulativa
ys = normalize(unbias(ys), self.amp) # normalizza tra -1 e 1
return ys
Forma d'onda.
sig = pym.BrownianNoise()
wave = sig.make_wave(0.5, 11025)
wave.plot(color="red",linewidth=1)
Spettro.
Se realizziamo uno spettrogramma lineare del rumore rosso non otteniamo una visualizzazione soddisfacente in quanto tutta l'energia è alle basse frequenze mentre le componenti più acute non sono visualizzate.
spek = wave.make_spectrum()
spek.plot_power(y_lim=[0,10000],high=2000,color="red",linewidth=0.5) # plot_power
Per migliorare la visualizzazione possiamo calcolare sia le frequenze che le ampiezze su una scala logaritmica.
spek.plot_power(y_lim=[10**-5,10**7],curva='log',color="red",linewidth=0.3) # plot_power
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Aggiungiamo alla classe _Spectra un nuovo metodo che calcola la curva stimata nel rapporto ampiezza/frequenza.
class _Spectra(): # Classe Privata
"""Contiene codice comune a Spectrum e DTC"""
def __init__(self, hs, fs, framerate, full=False):
"""Inizializza uno spettro.
hs: array di ampiezze (reali o complesse)
fs: array of frequenze (bins)
framerate: frames per secondo
full: boolean per indicare full FFT o FFT reale
"""
self.hs = np.asanyarray(hs)
self.fs = np.asanyarray(fs)
self.framerate = framerate
self.full = full
@property
def max_freq(self): # Riporta la Frequenza di Nyquist
return self.framerate / 2
@property
def amps(self): # Riporta le ampiezze dei bins
return np.absolute(self.hs)
@property
def power(self): # Riporta le magnitudini
return self.amps ** 2
def render_full(self, high=None): # Estrae ampiezze e frequenze da un full spectrum
hs = np.fft.fftshift(self.hs)
amps = np.abs(hs)
fs = np.fft.fftshift(self.fs)
i = 0 if high is None else find_index(-high, fs)
j = None if high is None else find_index(high, fs) + 1
return fs[i:j], amps[i:j]
def plot(self, high=None,y_lim=[0,1],soglia=1,curva="linear",**kvargs): # High massima frequenza
if self.full: # y_lim limite di visualizzazione ampiezze
fs, amps = self.render_full(high) # soglia = per eliminare rumore di fondo
amps_id = amps > soglia # Array di 0 e 1
amps_clean = amps * amps_id # Taglia quelli sotto la soglia
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(fs, amps_clean, **kvargs)
else:
i = None if high is None else find_index(high, self.fs)
amps_id = self.amps > soglia
amps_clean = self.amps * amps_id
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.fs[:i], amps_clean[:i],**kvargs)
def plot_power(self, high=None,y_lim=[0,1],soglia=1,curva="linear",**kvargs):
if self.full:
fs, amps = self.render_full(high)
amps_id = amps > soglia
amps_clean = amps * amps_id
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(fs, amps_clean ** 2, **kvargs)
else:
i = None if high is None else find_index(high, self.fs)
plt.ylim(y_lim)
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.fs[:i], self.power[:i],**kvargs)
def estimate_slope(self):
"""Esegue una regressione lineare su log power vs log frequency.
returns: slope, inter, r2, p, stderr
a noi interessa solo slope
"""
x = np.log(self.fs[1:])
y = np.log(self.power[1:])
t = scipy.stats.linregress(x, y)
return t
class Spectrum(_Spectra): # Sottoclasse
"""Rappresenta lo spettro di un segnale"""
def __len__(self): # Numero di bins
return len(self.hs)
def scale(self, factor):
self.hs *= factor
def make_integrated_spectrum(self):
"""Genera il plot dello spettro integrale.
"""
cs = np.cumsum(self.power) # Somma cumulativa delle ampiezze (power ereditato da _Spectra())
cs /= cs[-1] # Divide per l'ultimo elemento riscalando tra 0 e 1
return IntegratedSpectrum(cs, self.fs)
sig = pym.BrownianNoise()
wave = sig.make_wave(0.5, 11025)
spek = wave.make_spectrum()
slope = spek.estimate_slope() # slope = -1.8
print(slope)
LinregressResult(slope=-1.8165923819408223, intercept=14.022311779810332, rvalue=-0.81074111489991, pvalue=0.0, stderr=0.024994798670249303, intercept_stderr=0.19198525391203583)
In questo modo possiamo notare che il rapporto tra energia e frequenza che definisce la curva tipica del rumore rosso è data dalla formula:
$$a = 1/freq^2$$Questo è il motivo per il quale si chiama rumore rosso (e non marrone) in quanto se combiniamo la luce visibile con un energia proporzionale alla stessa formula otteniamo il rosso che è alle basse frequenze dello spettro.
Pink noiseIndice
Rumore rosa che possiamo definire anche come rumore non uniforme correlato.
La relazione che intercorre tra energia e frequenza del rumore bianco e del rumore rosso è data dall'esponente $\beta$ che nel primo caso è $0$:
$$a = 1/freq^0$$il cui risulato la definizione di un valore medio di energia costante per tutte le frequenze mentre nel secondo caso è $2$:
$$a = 1/freq^2$$che invece disegna una curva discendente all'aumentare delle frequenze.
Il rumore rosa invece è caratterizzato da una curva definita da un esponente $\beta$ compreso tra 0 e 2:
$$a = 1/freq^\beta$$Esistono diversi modi per generare rumore rosa, il più semplice consiste nell'applicare un filtro con la curva di taglio desiderata ad un rumore bianco.
Definiamo una classe figlia di _Noise che al suo interno realizzi le seguenti operazioni:
- Genera la forma d'onda di un rumore bianco (dominio del tempo).
- La trasforma in spettro (dominio delle frequenze).
- Lo filtra in accordo ad una curva di taglio - aggiungiamo il metodo pink_filter alla classe Spectrum.
- Lo trasforma nuovamente in segnale (dominio del tempo) - aggiungiamo il metodo make_wave alla classe Spectrum.
N.B. aggiungiamo anche il metodo unbias ( che rimuove eventuali DC offsets ) a Wave.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def __add__(self, other):
"""Somma due wave campione per campione.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n)
ts = start + np.arange(n) / self.framerate
def add_ys(wave):
i = find_index(wave.start, ts)
diff = ts[i] - wave.start
dt = 1 / wave.framerate
if (diff / dt) > 0.1:
warnings.warn(
"Non posso sommare; il loro " "tempo non coincide."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
n = len(self.ys)
d = 1 / self.framerate
if full:
hs = np.fft.fft(self.ys)
fs = np.fft.fftfreq(n, d)
else:
hs = np.fft.rfft(self.ys)
fs = np.fft.rfftfreq(n, d)
return Spectrum(hs, fs, self.framerate, full)
def make_sonogram(self, wsize, win_flag=True):
if win_flag:
window = np.hamming(wsize)
i, j = 0, wsize
step = int(wsize // 2)
spec_map = {}
while j < len(self.ys):
segment = self.slice(i, j)
if win_flag:
segment.window(window)
t = (segment.start + segment.end) / 2
spec_map[t] = segment.make_spectrum()
i += step
j += step
return Sonogram(spec_map, wsize)
def unbias(self):
"""Richiama la funzione che rimuove i DC offsets.
"""
self.ys = unbias(self.ys)
class Spectrum(_Spectra):
"""Rappresenta lo spettro di un segnale"""
def __len__(self): # Numero di bins
return len(self.hs)
def scale(self, factor):
self.hs *= factor
def make_integrated_spectrum(self):
cs = np.cumsum(self.power)
cs /= cs[-1]
return IntegratedSpectrum(cs, self.fs)
def pink_filter(self, beta=1): # Metodo aggiunto
"""Applica un filtro per il pink noise.
beta: esponente di f^beta/2
"""
denom = self.fs ** (beta / 2.0) # radice delle frequenze
denom[0] = 1 # assegna 1 a f=0
self.hs /= denom # divide le ampiezze per la radice delle frequenze
def make_wave(self):
"""Trasforma lo spettro nel dominio del tempo.
returns: Wave
"""
if self.full: # da _Spectra (full oppure real FFT)
ys = np.fft.ifft(self.hs)
else:
ys = np.fft.irfft(self.hs)
# NOTE: nella trasformata inversa perdiamo lo start time;
# possiamo rimediare salvandolo in Spectrum
#ts = self.start + np.arange(len(ys)) / self.framerate
return Wave(ys, framerate=self.framerate)
class PinkNoise(_Noise):
"""Rappresenta rumore rosa."""
def __init__(self, amp=1.0, beta=1.0):
"""
amp: float amplitude, 1.0 is nominal max
beta: esponente della curva di taglio
"""
self.amp = amp
self.beta = beta
def make_wave(self, duration=1, start=0, framerate=11025):
"""Esattamente come il make_wave di Signal
returns: Wave
"""
signal = WhiteNoise() # Rumore bianco
wave = signal.make_wave(duration, start, framerate) # Wave
spectrum = wave.make_spectrum() # Spectrum (tempo --> frequenze)
spectrum.pink_filter(beta=self.beta) # Filtro (nuovo metodo di Spectrum)
wave2 = spectrum.make_wave() # Wave (frequenze --> tempo)
wave2.unbias() # Unbias (media a 0)
wave2.normalize(self.amp) # Normalizza
return wave2
Forma d'onda.
sig = pym.PinkNoise()
wave = sig.make_wave(0.5, 11025)
wave.plot(color="red",linewidth=0.5)
Notiamo come la forma d'onda sia simile a quella del rumore rosso ma più randomica evidenziando possibili correlazioni tra i valori.
dur = wave.duration # Otteniamo la durata in secondi
fad = 0.02 # Definiamo un tempo di fade
rate = wave.framerate # Otteniamo la framerate
env = pym.fade(dur, fad, rate) # Definiamo un inviluppo
wave.window(env) # applichiamo l'inviluppo a wave
wave.make_audio()
Spettro.
Visualizziamo i tre rumori su scala logaritmica.
w = pym.WhiteNoise()
ww = w.make_wave(0.5, 11025)
ws = ww.make_spectrum()
p = pym.PinkNoise()
pw = p.make_wave(0.5, 11025)
ps = pw.make_spectrum()
b = pym.BrownianNoise()
bw = b.make_wave(0.5, 11025)
bs = bw.make_spectrum()
ws.plot_power(y_lim=[10**-3,10**7],curva='log',color="gray",linewidth=0.5,alpha=0.7)
ps.plot_power(y_lim=[10**-3,10**7],curva='log',color="pink",linewidth=0.5,alpha=0.7)
bs.plot_power(y_lim=[10**-3,10**7],curva='log',color="red",linewidth=0.5,alpha=0.7)
Gaussian NoiseIndice
Abbiamo visto come il rumore bianco è un rumore non correlato con distribuzione uniforme.
Definiamo una classe ( identica a WhiteNoise ).
class UncorrelatedUniformNoise(_Noise):
"""Rumore non correlato con distribuzione uniforme"""
def evaluate(self, ts):
ys = np.random.uniform(-self.amp, self.amp, len(ts))
return ys
sig = pym.UncorrelatedUniformNoise()
wave = sig.make_wave(0.5, 11025)
spek = wave.make_spectrum()
spek.plot_power(y_lim=[10**0,10**5],curva='log',color="gray",linewidth=0.5)
Quando parliamo di rumore bianco però spesso ci riferiamo senza saperlo a un rumore non correlato con distribuzione gaussiana ( normale ) avente il valore medio di 0 e una deviazione standard che corrisponde all'ampiezza.
In teoria il range dei valori può essere compreso tra $-inf$ e $+inf$ ma ci aspettiamo che sia al 99% tra -3 e +3.
Questo tipo di segnale ha una proprietà interessante: sia i valori di ampiezza istantanea sia l'energia nello spettro sono un rumore gaussiano.
class UncorrelatedGaussianNoise(_Noise):
"""Rumore non correlato con distribuzione uniforme"""
def evaluate(self, ts):
ys = np.random.normal(-self.amp, self.amp, len(ts))
return ys
sig = pym.UncorrelatedGaussianNoise()
wave = sig.make_wave(0.5, 11025)
spek = wave.make_spectrum()
spek.plot_power(y_lim=[10**0,10**5],curva='log',color="gray",linewidth=0.5)
Esercizi 4Indice
- Scaricare alcuni soundfiles dal sito https://asoftmurmur.com/ contenente registrazioni di rumori naturali.
- Computare e visualizzare lo spettro e identificare a quale tipo di rumore corrisponde per ogni registrazione.
- Estrarre un frammento e computarne la forma d'onda.
- Cercare un sito da cui scaricare lo storico del prezzo giornaliero di un BitCoin come CSV file.
- Importare il file, computare e visualizzare lo spettro e identificare a quale tipo di rumore corrisponde.
- Un contatore Geiger misura le radiazioni. Quando una particella ionizzata colpisce il sensore questo produce un impulso di corrente. Il segnale risultante può essere descritto come una distribuzione di Poisson non correlata che corrisponde al numero di particelle rilevate in un intervallo di tempo.
- Scrivere una classe derivata da _Noise definendo un metodo evaluate che impieghi np.random.poisson per generare i valori randomici. Il parametro lam di questa funzione corrisponde alla media del numero di particelle in ogni intervallo. Potete utilizzare un Attributo 'amp' per specificare 'lam'. Ad esempio se la rata di campionamento è 10.000 Hz e amp è 0.001 possiamo aspettarci circa 10 "clicks" per secondo. Computare soundfiles di un secondo di rumore con diversi parametri e descrivere le differenze.
AutocorrelazioneIndice
Abbiamo definito il rumore bianco come non correlato ovvero ogni valore è indipendente rispetto agli altri.
Abbiamo definito il rumore rosso come correlato in quanto ogni valore dipende dal precedente.
Definiamo in modo più preciso questi termini esploriando la funzione di autocorrelazione che è uno strumento utile per l'analisi dei segnali.
Indice di correlazioneIndice
Correlazione tra variabili significa che se conosciamo il valore di una possiamo ricavare informazioni anche sull'altra.
Il metodo più comune per quantificare la correlazione è l'indice di correlazione di Pearson usualmente associato alla lettera $\rho$ (rho).
Per due variabili ognuna delle quali contiene $N$ valori:
$$\rho = \frac{\sum_{i}(x_{i} - \mu_{x})(y_{i} - \mu_{y})}{N\sigma_{x}\sigma_{y}}$$dove $\mu_{x}$ (mu) e $\mu_{y}$ sono la media di $x$ e $y$ mentre $\sigma_{x}$ (sigma) e $\sigma_{y}$ la loro deviazione standard.
L'indice di correlazione di Pearson è sempre tra $-1$ e $+1$.
Se $\rho$ è positivo l'indice di correlazione sarà positivo ovvero se una variabile è alta l'altra tenderà ad essere alta.
Se $\rho$ è negativo l'indice di correlazione è negativo ovvero se una variabile è alta l'altra tenderà ad essere bassa.
Il valore di $\rho$ definisce la quantità di correlazione.
Se $\rho$ è $1$ oppure $-1$ le variabili sono perfettamente correlate ovvero se conosciamo il valore di una possiamo fare una perfetta previsione dell'altra.
Se $\rho$ invece è vicino allo $0$ la correlazione bassa e le conoscenza di una ci dice poco riguardo all'altra.
Python fornisce diversi oggetti per calcolare l'indice di correlazione, noi utilizzeremo np.corrcoeff che accetta qualsiasi numero di variabili e restituisce una matrice di correlazioni.
Facciamo un esempio con due variabili.
Definiamo una funzione che genera due sinusoidi con fase iniziale differente.
def sin_wave(freq=440, duration=1, offset=0):
"""Genera un'onda sinusoidale.
freq: float cps
duration: float secondi
offset: float radianti
returns: Wave
"""
signal = Sinusoid(freq, offset=offset)
wave = signal.make_wave(duration)
return wave
sin1 = pym.sin_wave(freq=4,offset=0)
sin2 = pym.sin_wave(freq=4,offset=0.32*np.pi)
corr_mtx = np.corrcoef(sin1.ys, sin2.ys) # Calcola una matrice di correlazioni
print(corr_mtx)
sin1.plot()
sin2.plot()
[[1. 0.53582679] [0.53582679 1. ]]
Il valore $1.$ del primo subarray è l'indice di correlazione del primo segnale con se stesso.
Il valore $0.53$ del primo subarray è l'indice di correlazione del primo segnale con il secondo segnale.
Il valore $0.53$ del secondo subarray è l'indice di correlazione del secondo segnale con il primo segnale.
Il valore $1.$ del secondo subarray è l'indice di correlazione del secondo segnale con se stesso.
$0.53$ definisce una correlazione moderata.
All'aumentare dell'offset di fase l'indice di correlazione diminuisce fino a quando le due onde sono fuori fase di 180° ($-1.0$) per poi aumentare fino a raggiungere un offset di 360° (tornano coincidenti) disegnando un coseno.
Definiamo un nuovo mentodo di Wave che calcola l'indice di correlazione tra due onde.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def __add__(self, other):
"""Somma due wave campione per campione.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n)
ts = start + np.arange(n) / self.framerate
def add_ys(wave):
i = find_index(wave.start, ts)
diff = ts[i] - wave.start
dt = 1 / wave.framerate
if (diff / dt) > 0.1:
warnings.warn(
"Non posso sommare; il loro " "tempo non coincide."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
n = len(self.ys)
d = 1 / self.framerate
if full:
hs = np.fft.fft(self.ys)
fs = np.fft.fftfreq(n, d)
else:
hs = np.fft.rfft(self.ys)
fs = np.fft.rfftfreq(n, d)
return Spectrum(hs, fs, self.framerate, full)
def make_sonogram(self, wsize, win_flag=True):
if win_flag:
window = np.hamming(wsize)
i, j = 0, wsize
step = int(wsize // 2)
spec_map = {}
while j < len(self.ys):
segment = self.slice(i, j)
if win_flag:
segment.window(window)
t = (segment.start + segment.end) / 2
spec_map[t] = segment.make_spectrum()
i += step
j += step
return Sonogram(spec_map, wsize)
def unbias(self):
self.ys = unbias(self.ys)
def corr(self, other):
"""Calcola la correlazione tra due Waves.
other: Wave
returns: float indice di correlazione
"""
corr = np.corrcoef(self.ys, other.ys)[0, 1]
return corr
sin1 = pym.sin_wave(freq=4,offset=0)
sin2 = pym.sin_wave(freq=4,offset=0.32*np.pi)
sin1.corr(sin2) # invoca il metodo
0.5358267949789968
Correlazione seriale e autocorrelazioneIndice
I segnali spesso rappresentano la misurazione di quantità che variano nel tempo come le variazioni di pressione atmosferica o di voltaggio.
La correlazione seriale misura l'indice di correlazione tra elementi contigui (quello prima o quello dopo).
Nel caso di un segnale digitale dobbiamo:
- duplicare il segnale.
- shiftarlo di un campione avanti o indietro.
- calcolare l'indice di correlazione.
def serial_corr(wave, lag=1): # lag = di quanti elementi shiftare
n = len(wave) # Numero di elementi
y1 = wave.ys[lag:] # Parte dall'indice 1 fino alla fine (shift di 1)
y2 = wave.ys[:n-lag] # Parte dall'indice 0 fino al penultimo
corr = np.corrcoef(y1,y2)[0,1] # calcola l'indice
return corr
Testiamo questa funzione con i diversi tipi di noise illustrati nel paragrafo precedente.
w = pym.WhiteNoise()
ww = w.make_wave(0.5, 11025)
p = pym.PinkNoise()
pw = p.make_wave(0.5, 11025)
b = pym.BrownianNoise()
bw = b.make_wave(0.5, 11025)
print(pym.serial_corr(ww)) # Indice di correlazione seriale del rumore bianco
print(pym.serial_corr(pw)) # Indice di correlazione seriale del rumore rosa
print(pym.serial_corr(bw)) # Indice di correlazione seriale del rumore rosso
-0.0006529817509238741 0.7759442244966372 0.9989869485615911
L'autocorrelazione invece non è altro che il calcolo della correlazione tra il segnale originale e la sua copia shiftata con un lag variabile da 0 alla metà del segnale stesso.
Otteniamo un array che contiene una sequenza di indici di correlazione, uno per ogni lag.
Testiamolo con un rumore rosa aventi diversi valori di $\beta$ ( 0.0=rumore bianco, 1=rumore rosa, 2=rumore rosso ).
def autocorr(wave):
lags = range(len(wave.ys)//2) # genera una sequenza di lag (shift) da 0 alla metà dei campioni del segnale
corrs = [serial_corr(wave, lag) for lag in lags]
return lags, corrs
sig1 = pym.PinkNoise(beta=0.3).make_wave(1, 11025)
sig2 = pym.PinkNoise(beta=1.0).make_wave(1, 11025)
sig3 = pym.PinkNoise(beta=1.7).make_wave(1, 11025)
plt.ylim(0, 1.0)
plt.plot(pym.autocorr(sig1)[1],color='gray') # beta = 0.3
plt.plot(pym.autocorr(sig2)[1],color='pink') # beta = 1.0
plt.plot(pym.autocorr(sig3)[1],color='red') # beta = 1.7
[<matplotlib.lines.Line2D at 0x1538f8150>]
Osserviamo:
- per valori bassi di $\beta$ (rumore bianco) il segnale è poco correlato e diminuisce velocemente all'aumentare del lag.
- per valori più alti di $\beta$ (rumore rosa e rosso) la correlazione è maggiore e diminuisce più lentamente all'aumentare del lag.
Questo fenomeno si chiama dipendenza a lungo raggio perchè indica che ogni valore dipende da molti valori precedenti.
Autocorrelazione di segnali periodici e stima del pitchIndice
Osserviamo un utilizzo pratico legato al calcolo dell'autocorrelazione: la stima del pitch di un suono periodico.
Visualizziamo uno spettrogramma di una voce che glissa.
wave = pym.read_wave('suoni/vocegliss.wav') # genera un'istanza di Wave dal sound file
spek = wave.make_sonogram(wsize=2048)
spek.plot(high=4000)
wave.make_audio()
Possiamo osservare che la fondamentale glissa più o meno da 500 Hz fino a 300 Hz ovvero da Do5 a Mi4.
Per stimare il pitch in un punto del tempo possiamo utilizzare lo spettro ma il risultato non sempre è soddisfacente.
Come esempio selezioniamo un breve segmento da Wave e facciamo il plot dello spettro.
segmento = wave.segment(start=0.2,duration=0.01) # da 0.2 secondi per una durata di 0.1 secondi
spek = segmento.make_spectrum()
spek.plot(high=1000,y_lim=[0,60])
segmento.make_audio()
Dallo spettrogramma possiamo notare che c'è un picco attorno ai 400 Hz ma è difficile identificare l'altezza con precisione.
Il segmento analizzato ha un size di 441 campioni con una rata di campionamento a 44.100 Hz, quindi secondo il limite di Gabor la risoluzione in frequenza è di 100 Hz.
Questo significa che potrebbe esserci un'errore di 50 Hz in entrambe i lati ovvero cadere tra 350 e 450 Hz che in termini musicali a quelle frequenze corrispondono a 5 semitoni (moltissimo).
Per diminuire l'errore potremmo utilizzare una finestra più grande ma, trattandosi di un glissato comprenderebbe più cambiamenti frequenziali che comporterebbero una maggiore distribuzione dell'energia e dunque una minore precisione.
Possiamo stimare l'altezza di un suono in modo più preciso attraverso l'autocorrelazione.
Se un segnale è periodico ci aspettiamo la massima autocorrelazione quando il lag è uguale al periodo.
Visualizziamo un plot di due segmenti diversi dalla stessa registrazione a distanza di 0.0023 secondi.
def plot_shifted(wave, offset=0.0023, start=0.2):
segmento1 = wave.segment(start=start, duration=0.01) # primo segmento a 0.2 secondi
segmento2 = wave.segment(start=start-offset,duration=0.01) # secondo a 0.2-0.0023 secondi
segmento2.shift(offset) # riallinea nello stesso istante
segmento1.plot(linewidth=1.5,alpha=0.8)
segmento2.plot(linewidth=1.5,alpha=0.4)
corr = segmento1.corr(segmento2)
return corr
pym.plot_shifted(wave)
0.9885698349033551
I segmenti sono molto simili e la loro correlazione è di circa 0.99 il che suggerisce che il periodo è circa 0.0023 secondi.
Possiamo calcolare la frequenza $f = 1/T$ che in questo caso è: $1/0.0023 = 435$ ca.
In questo caso abbiamo stimato un periodo per tentativi ed errori ma possiamo automatizzare il processo con la funzione di autocorrelazione.
lags, corrs = pym.autocorr(segmento) # calcola l'autocorrelazione del segmento
plt.plot(lags,corrs) # visualizza l'andamento della correlazione (220 lag, la metà del size)
[<matplotlib.lines.Line2D at 0x1527aaad0>]
Ricordiamo che il grafico rappresenta l'andamento dell'indice di correlazione.
Il punto successivo al primo in cui la correlazione è massima arriva a lag = 101 (asse delle x).
Possiamo calcolare la frequenza corrispondente.
periodo = 101 / segmento.framerate
freq = 1 / periodo
print(freq, 'Hz')
436.63366336633663 Hz
Per verificare la precisione della stima possiamo calcolare la correlazione con lag 102 e 100 (i vicini) che restituisce 432 e 441 Hz.
L'errore con questo metodo è dunque compreso in meno di di 10 Hz (in termini musicali 30 cents o 1/3 di semitono) che è decisamente più accettabile dei 100 Hz dell'analisi spettrale.
Esercizi 5Indice
- Abbiamo vsito come utilizzare l'autocorrelazione per cercare il pitch stimato della fonadamentale.
- Scrivere una funzione chiamata pitchFollower e usarla per un test con un soundfile.
- Computare e visualizzare uno spettrogramma e confrontare i risultati.
- In uno degli esercizi precedenti abbiamo scaricato un file CSV con l'andamento dei prezzi di BitCoin e stimato lo spettro dei cambiamenti del prezzo.
- Computiamo l'autocorrelazione alla ricerca di qualche periodicità.
Trasformata discreta dei coseni (DCT)Indice
Questo tipo di trasformata è utilizzata nei formati di compressione come mp3 e suoi derivati per l'audio, JPEG per le immagini e MPEG per il video.
Per comprenderla seguiamo i seguenti passi:
Sintesi - definiamo dei parziali attraverso due insiemi uno per le frequenze e uno per le ampiezze. Come possiamo costruire una forma d'onda partendo da questi dati? Risolviamo questo problema in modo tradizionale attraverso la somma di segnali sinusoidali.
Risolviamo il problema del punto precedente attraverso un metodo alternativo e più performante impiegando numpy array.
Analisi - definiamo un segnale e un insieme di frequenze. Come possiamo trovare l'ampiezza di ognuna di queste?
Risolviamo il problema del punto precedente impiegando l'algebra linerare per migliorare l'efficenza di calcolo.
SintesiIndice
Disegnamo la forma d'onda risultante attraverso la sintesi additiva tradizionale.
Definiamo la funzione sintesi1 che accetta come attributi una lista di ampiezze, una di frequenze (fs) e una di onsets (ts) nella quale:
- generiamo un array di istanze di Sinusoid (componenti).
- sommiamo tra di loro i parziali con SumSignal che avevamo definito qui.
Restituisce una lista di ampiezze istantanee (ys).
def sintesi1(amps, fs, ts):
componenti = [pym.Sinusoid(freq, amp, func=np.cos) # Genera i parziali
for amp, freq in zip(amps, fs)] # zip() crea una tuple da elementi di due array diversi
signal = pym.SumSignal(*componenti) # * = numero indefinito di attributi
ys = signal.evaluate(ts)
return ys
amps = np.array([0.4, 0.25,0.1, 0.05, 0.2]) # Somma deve dare 1.0
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate) # Array di onsets - definisce la durata (1 secondo)
ys = pym.sintesi1(amps, fs, ts) # Genera l'array di ampiezze istantanee
wave = pym.Wave(ys,framerate=framerate) # Genera una Wave
wave.make_audio()
wave = wave.segment(0,0.02)
wave.plot()
Sintesi con np.array
Vediamo un metodo alternativo per lo stesso tipo di sintesi più efficente per quanto riguarda la computazione e che ci tornerà utile per l'analisi.
amps = np.array([0.4, 0.25,0.1, 0.05, 0.2]) # Somma deve dare 1.0
fs = [200, 300, 400, 500, 600] # 5 elementi
ts = np.linspace(0,1,8) # 8 elementi
print(ts)
[0. 0.14285714 0.28571429 0.42857143 0.57142857 0.71428571 0.85714286 1. ]
Calcoliamo il prodotto diadico tra onsets e frequenze ottenendo un array 2D dove ogni riga è un array contenente il prodotto delle frequenze dei parziali per gli istanti di tempo. $$ts[i] * [fs]$$
$$0.00000000 * [200, 300, 400, 500, 600]$$$$0.14285714 * [200, 300, 400, 500, 600]$$$$0.28571429 * [200, 300, 400, 500, 600]$$$$...$$args = np.outer(ts,fs) # Calcola il prodotto diadico
print(args)
[[ 0. 0. 0. 0. 0. ] [ 28.57142857 42.85714286 57.14285714 71.42857143 85.71428571] [ 57.14285714 85.71428571 114.28571429 142.85714286 171.42857143] [ 85.71428571 128.57142857 171.42857143 214.28571429 257.14285714] [114.28571429 171.42857143 228.57142857 285.71428571 342.85714286] [142.85714286 214.28571429 285.71428571 357.14285714 428.57142857] [171.42857143 257.14285714 342.85714286 428.57142857 514.28571429] [200. 300. 400. 500. 600. ]]
Moltiplichiamo gli array per $2\pi$ e calcoliamone il $\cos$ in modo che ogni elemento sia il risultato di:
$$\cos(2\pi ft)$$che è la funzione d'onda della cosinusoide.
M = np.cos(PI2 * args)
print(M)
print(amps)
[[ 1. 1. 1. 1. 1. ] [-0.90096887 0.6234898 0.6234898 -0.90096887 -0.22252093] [ 0.6234898 -0.22252093 -0.22252093 0.6234898 -0.90096887] [-0.22252093 -0.90096887 -0.90096887 -0.22252093 0.6234898 ] [-0.22252093 -0.90096887 -0.90096887 -0.22252093 0.6234898 ] [ 0.6234898 -0.22252093 -0.22252093 0.6234898 -0.90096887] [-0.90096887 0.6234898 0.6234898 -0.90096887 -0.22252093] [ 1. 1. 1. 1. 1. ]] [0.4 0.25 0.1 0.05 0.2 ]
Ogni colonna contiene i valori dei campioni (ys) nella sequenza dei tempi (ts) di una cosinusoide alla frequenza specificata (5 colonne per 5 frequenze).
Infine riscaliamo i valori per le ampiezze con np.dots che moltiplica ogni elemento di un'array per ogni elemento di un'altro array e poi somma tra loro gli elementi dell'array risultante ottenendo il valore del campione in quell'istante.
$$\sum (M[i] * [amps])$$$$[ 1.0, 1.0, 1.0, 1.0, 1.0 ] * [ 0.4, 0.25, 0.1, 0.05, 0.2 ] = [ 0.4 + 0.25 + 0.1 + 0.05 + 0.2 ] = 1.$$$$[-0.9,0.6,0.6,-0.9,-0.2] * [ 0.4,0.25,0.1,0.05,0.2 ] = [-0.3 + 0.1 + 0.06 + -0.04 + -0.04] = -0.23$$Se effettuiamo il calcolo ad ogni onset otteniamo la forma d'onda risultante.
ys = np.dot(M, amps)
print(ys)
[ 1. -0.23171875 0.02249431 -0.29077556 -0.29077556 0.02249431 -0.23171875 1. ]
Possiamo ora definire la funzione sintesi2 che include tutto il procedimento appena descritto.
def sintesi2(amps, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # sin(2pi*f*t)
ys = np.dot(M, amps) # riscala le ampiezze
return ys # campioni
amps = np.array([0.4, 0.25, 0.1, 0.05, 0.2]) # Somma deve dare 1.0
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate) # Array di onsets (inizio, fine, numero_di_elementi) - definisce la durata
ys = pym.sintesi2(amps, fs, ts) # Genera l'array di ampiezze istantanee
wave = pym.Wave(ys,framerate=framerate) # Genera una Wave
wave.make_audio()
wave = wave.segment(0,0.02)
wave.plot()
Confrontiamo i due risultati
amps = np.array([0.4, 0.25, 0.1, 0.05, 0.2]) # Somma deve dare 1.0
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate)
ys1 = pym.sintesi1(amps, fs, ts)
ys2 = pym.sintesi2(amps, fs, ts)
max(abs(ys1 - ys2)) # la massima variazione
2.523536934972981e-13
La maggiore differenza tra le due tecniche è infinitesimamente piccola e dovuta agli errori di approssimazione dei decimali.
Scrivere la computazione in termini di algebra lineare rende il codice più snello e veloce in quanto effettua operazioni su matrici e vettori.
Possiamo definire algebricamente sintesi2:
$$M = cos(2\pi t \otimes f)$$$$y = Ma$$- $a$ = vettore di ampiezze
- $t$ = vettore di tempi
- $f$ = vettore di frequenze
- $\otimes$ = prodotto diatico di due vettori
Possiamo considerare i np.array come vettori in $R^n$ in quanto ogni elemento è definito da due valori che sono indice e valore.
AnalisiIndice
Partiamo dal presupposto di avere un segnale audio che sappiamo definito dalla somma di cosinusoidi ognuna con una propria frequenza.
Come possiamo ricavare le ampiezze di ognuna di queste frequenze?
O meglio se conosciamo ys, ts e fs come possiamo ottenere amps?
In termini di algebra lineare la prima equazione è identica a quella per la sintesi:
$$M = cos(2\pi t \otimes f)$$Dopodichè dobbiamo calcolare la variabile $a$ dall'espressione $y = Ma$ o in altre parole risolvere un sistema lineare in quanto abbiamo due incognite ($y$ e $a$).
Ma cosa significa risolvere un sistema lineare?
Un'equazione di primo grado può avere:
- una incognita $x = 13$
- più incognite $2x + 4y = -2$
Prendiamo due equazioni come esempio:
$$x + y = 24$$$$x - y = 6$$singolarmente ognuna di queste equazioni ha infinite soluzioni: (0, 24) (1, 23) (-26, 50)... danno tutte come somma 24 mentre (7, 1) (8, 2) (27, 21)...danno come risultato 6.
Se invece vogliamo due risultati (x e y) che le soddisfano entrambe dobbiamo scrivere un sistema:
$$\begin{cases}x + y = 24 \\ x - y = 6 \end{cases}$$in questo caso un sistema 2x2 ovvero 2 incognite per 2 equazioni che possiamo anche considerare una matrice.
Si dice sistema lineare in quanto tutti i termini hanno esponente 1.
Ci sono diversi modi di risolvere i sistemi lineari, numpy utilizza linalg.solve.
Definiamo una funzione che effettua i calcoli.
def analisi1(ys, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # cos(2pi*f*t)
amps = np.linalg.solve(M, ys) # calcola le ampiezze
return amps
Valutiamo la funzione anche se ci darà errore.
amps = np.array([0.4, 0.25, 0.1, 0.05, 0.2])
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate)
ys = pym.sintesi2(amps, fs, ts) # Sintesi
a = pym.analisi1(ys, fs, ts)
print(a)
--------------------------------------------------------------------------- LinAlgError Traceback (most recent call last) Cell In[133], line 8 5 ts = np.linspace(0,1,framerate) 6 ys = pym.sintesi2(amps, fs, ts) # Sintesi ----> 8 a = pym.analisi1(ys, fs, ts) 9 print(a) File ~/Desktop/musicaecodice/anew/dspy/moduli/pym.py:994, in analisi1(ys, fs, ts) 992 args = np.outer(ts,fs) # f*t ad ogni ts 993 M = np.cos(PI2 * args) # cos(2pi*f*t) --> 994 amps = np.linalg.solve(M, ys) # calcola le ampiezze 995 return amps File <__array_function__ internals>:200, in solve(*args, **kwargs) File ~/anaconda3/lib/python3.11/site-packages/numpy/linalg/linalg.py:373, in solve(a, b) 371 a, _ = _makearray(a) 372 _assert_stacked_2d(a) --> 373 _assert_stacked_square(a) 374 b, wrap = _makearray(b) 375 t, result_t = _commonType(a, b) File ~/anaconda3/lib/python3.11/site-packages/numpy/linalg/linalg.py:190, in _assert_stacked_square(*arrays) 188 m, n = a.shape[-2:] 189 if m != n: --> 190 raise LinAlgError('Last 2 dimensions of the array must be square') LinAlgError: Last 2 dimensions of the array must be square
Leggendo l'errore capiamo che la soluzione di un sistema lineare è corretta solo se la matrice è un quadrato ovvero quando il numero di equazioni coincide con il numero delle incognite mentre nel nostro caso le equazioni M sono 11.025 (ts) mentre le incognite 5 (fs).
In questo caso sappiamo che i valori ys sono stati generati specificando 5 frequenze quindi possiamo effettuare l'analisi con solo i valori dei primi 5 campioni (ys).
amps = np.array([0.4, 0.25, 0.1, 0.05, 0.2])
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate)
ys = pym.sintesi2(amps, fs, ts) # Sintesi
n = len(fs) # Numero di frequenze
a = pym.analisi1(ys[:n], fs, ts[:n]) # Slicing
print(a)
[0.4 0.25000001 0.09999999 0.05 0.2 ]
L'esecuzione della cella precedente prova la correttezza dell'analisi ma solo nei casi in cui conosciamo il numero di parziali che compongono lo spettro. Inoltre la computazione è molto lenta e proporzionale a $n^3$ dove $n$ è il numero delle colonne di $M$ (numero dei parziali).
Per ottimizzare il calcolo possiamo risolvere i sistemi lineari invertendo le matrici (metodo di Cramer).
L'inversione di una matrice $M$ è $M^{-1}$ e possiede la proprietà che $M^{-1}M = I$
M = np.array([[1,4,5],[3,6,4],[9,1,5]]) # Matrice
Mi = np.linalg.inv(M) # Matrice inversa (M^-1)
I = np.dot(Mi,M) # Mi * M elemento per elemento
print(M)
print(Mi)
print(np.round(I)) # Matrice d'identità (I)
[[1 4 5] [3 6 4] [9 1 5]] [[-0.17931034 0.10344828 0.09655172] [-0.14482759 0.27586207 -0.07586207] [ 0.35172414 -0.24137931 0.04137931]] [[ 1. -0. 0.] [-0. 1. 0.] [ 0. 0. 1.]]
Dove $I$ è la matrice d'identità in cui tutti gli elementi della diagonale hanno valore 1. mentre gli altri 0.
Per risolvere l'equazione $$y = Ma$$ possiamo moltiplicare entrambi i lati per $M^{-1}$:
$$M^{-1}y = M^{-1}Ma$$siccome $M^{-1}M = I$ $$M^{-1}y = Ia$$
siccome $I = 1.$ $$M^{-1}y = a$$
Per semplificare i calcoli dovendo utilizzare matrici quadrate impieghiamo:
- quattro ampiezze
- quattro campioni per unità di tempo
- quattro frequenze ricavate dividendo in quattro parti uguali (bins) la metà dello spettro (Nyquist).
amps = np.array([0.6, 0.25, 0.1, 0.05]) # Vettore di ampiezze
N = len(amps) # Numero di righe e colonne 4x4
time_unit = 0.001 # Millisecondi
ts = np.arange(N) / N * time_unit # Vettore di tempi (4 campioni siccome abbiamo 4 frequenze)
# da 0 all'unità di tempo scelta
max_freq = N / time_unit / 2 # Siccome la frame rate è N campioni per unità di tempo
# la frequenza di Nyquist è 4/0.001/2 = 2000 Hz
fs = np.arange(N) / N * max_freq # Frequenze [0 1 2 3] / 3 * 2000
ys = pym.sintesi2(amps, fs, ts) # ---------> Sintesi
# ---------> Analisi
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # sin(2pi*f*t)
Mi = np.linalg.inv(M) # Matrice inversa (M^-1)
a = np.dot(Mi, ys) # Ampiezze (M^-1*y = a)
print(a)
[0.6 0.25 0.1 0.05]
Invertire le matrici però è anch'essa un'operazione lenta a livello computazionale tranne che in alcuni casi speciali come le matrici ortogonali.
Se l'inversione di $M$ (ovvero $M^{-1}$) coincide con la sua matrice trasposta ($M^{T}$ - ovvero le righe diventano colonne e viceversa) possiamo definirla come matrice ortogonale e questa operazione in numpy è molto veloce.
Se la matrice è ortogonale: $$M^{-1} = M^{T}$$
abbiamo $$M^{T}M = I$$
Possiamo impiegare quest'ultimo calcolo per verificare se una matrice è ortogonale.
amps = np.array([0.6, 0.25, 0.1, 0.05]) # Vettore di ampiezze
N = len(amps) # Numero di righe e colonne 4x4
time_unit = 0.001 # Millisecondi
ts = np.arange(N) / N * time_unit # Vettore di tempi (4 campioni siccome abbiamo 4 frequenze)
# da 0 all'unità di tempo scelta
max_freq = N / time_unit / 2 # Siccome la frame rate è N campioni per unità di tempo
# la frequenza di Nyquist è 4/0.001/2 = 2000 Hz
fs = np.arange(N) / N * max_freq # Frequenze [0 1 2 3] / 3 * 2000
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # sin(2pi*f*t)
print(np.round(M, 3)) # Arrotonda
[[ 1. 1. 1. 1. ] [ 1. 0.707 0. -0.707] [ 1. 0. -1. -0. ] [ 1. -0.707 -0. 0.707]]
Notiamo che la matrice è simmetrica il che vuole dire che l'elemento (x, y) è uguale a quello (y, x) il che implica che $M$ coincide con la sua trasposizione ($M = M^{T}$) e dunque non è ortogonale.
Se infatti calcoliamo la matrice d'identità ($M^{T}M$) osserviamo che la diagonale non restituisce lo stesso valore.
I = np.dot(np.transpose(M), M) # M^T * M
print(np.round(I,3))
[[ 4. 1. -0. 1.] [ 1. 2. 1. -0.] [-0. 1. 2. 1.] [ 1. -0. 1. 2.]]
Se però scegliamo tempi (ts) e frequenze (fs) con accuratezza possiamo ottenere $M$ ortogonale.
Una possibilità consiste nel shiftare i tempi (ts) e le frequenze (fs) di mezza unità (0.5).
Questa operazione è chiamata DCT-IV ovvero la quarta di otto tipi diversi di DCT.
Semplifichiamo eliminando le unità di tempo.
amps = np.array([0.6, 0.25, 0.1, 0.05]) # Vettore di ampiezze
N = len(amps) # Numero di righe e colonne 4x4
ts = (0.5 + np.arange(N)) / N # Vettore di tempi shiftati
fs = (0.5 + np.arange(N)) / 2 # Vettore di Frequenze shiftate / 2 (Nyquist)
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # sin(2pi*f*t)
I = np.dot(np.transpose(M), M) # M^T * M
print(np.round(M,3)) # Simmetrico
print(np.round(I,3)) # Quasi ortogonale
[[ 0.981 0.831 0.556 0.195] [ 0.831 -0.195 -0.981 -0.556] [ 0.556 -0.981 0.195 0.831] [ 0.195 -0.556 0.831 -0.981]] [[ 2. -0. 0. 0.] [-0. 2. -0. -0.] [ 0. -0. 2. -0.] [ 0. -0. -0. 2.]]
Notiamo che questa matrice restituiscea $2I$ il che la rende quasi ortogonale mentre la presenza di $-0.$ è dovuta all'approssimazione del calcolo.
Siccome $M$ è simmetrico e quasi ortogonale, l'inverso di $M$ è $M/2$ (extra fattore).
A questo punto possiamo scrivere una versione efficente di analisi1.
def analisi2(ys, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # cos(2pi*f*t)
amps = np.dot(M, ys) / 2 # calcola le ampiezze e le divide per 2 per compensare l'extra fattore
return amps
amps = np.array([0.4,0.3,0.2,0.1])
N = len(amps)
ts = (0.5 + np.arange(N)) / N
fs = (0.5 + np.arange(N)) / 2
ys = pym.sintesi2(amps, fs, ts)
a = pym.analisi2(ys, fs, ts)
print(ys)
print(fs)
print(a)
[ 0.77237807 0.02234667 0.05015753 -0.02041955] [0.25 0.75 1.25 1.75] [0.4 0.3 0.2 0.1]
O meglio una funzione dct_IV nella quale non dobbiamo specificare ts e fs che saranno ricavati dal size di ys
def dct_IV(ys):
N = len(ys) # Numero di campioni
ts = (0.5 + np.arange(N)) / N # Frames
fs = (0.5 + np.arange(N)) / 2 # Frequenze (bins)
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # Fasi ad ogni ts cos(2pi*f*t)
amps = np.dot(M, ys) / 2 # calcola le ampiezze
return amps
amps = np.array([0.1, 0.3, 0.15, 0.25])
N = len(amps)
ts = (0.5 + np.arange(N)) / N
fs = (0.5 + np.arange(N)) / 2
ys = pym.sintesi2(amps, fs, ts)
a = pym.dct_IV(ys)
print(a)
[0.1 0.3 0.15 0.25]
DCT inversaIndice
Notiamo che le funzioni sintesi2 e analisi2 sono quasi identiche, l'unica differenza è che nella seconda funzione i valori sono dimezzati.
def sintesi2(amps, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # cos(2pi*f*t)
ys = np.dot(M, amps) # riscala le ampiezze
return ys # campioni
def analisi2(ys, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # cos(2pi*f*t)
amps = np.dot(M, ys) / 2 # calcola le ampiezze DIMEZZATE
return amps
Sfruttiamo questa caratteristica per calcolare la DCT inversa trasformando un vettore di ampiezze dei parziali in un array di ampiezze istantanee (ys).
def inverse_dct_IV(amps):
return dct_IV(amps) * 2
Confrontiamo i risulati per valutare l'entità di errore.
amps = [0.6,0.25,0.1,0.05] # Ampiezze dei parziali
ys = pym.inverse_dct_IV(amps) # Ampiezze istantanee (DCT inversa)
amps2 = pym.dct_IV(ys) # Ampiezze dei parziali risultanti dall'analisi
print(ys)
print(amps)
print(amps2)
print(max(abs(amps - amps2))) # Confronto con gli originali
[0.86165011 0.32425215 0.14922833 0.01226933] [0.6, 0.25, 0.1, 0.05] [0.6 0.25 0.1 0.05] 5.551115123125783e-17
Anche in questo caso l'errore è minimo.
Classe DCTIndice
Definiamo una classe simile a Spectrum (figlia di _Spectra) che possa essere richiamata anch'essa come metodo di Wave.
Utilizziamo l'oggetto scipy.fftpack.idct(self.hs, type=2) che computa in modo ottimizzato diversi tipi di DTC.
Il tipo II è quello più utilizzato.
class Dct(_Spectra):
"""Rappresenta lo spettro di un segnale tramite analisi/risintesi DCT"""
@property
def amps(self):
"""Sequenza di ampiezze dei parziali
Nota: le ampiezze sono numeri reali positivi o negativi.
"""
return self.hs
def __add__(self, other):
"""Somma due DCT elemento per elemento
other: DCT
returns: nuovo DCT con il risultato della somma
"""
if other == 0:
return self
assert self.framerate == other.framerate
hs = self.hs + other.hs
return Dct(hs, self.fs, self.framerate)
def make_wave(self):
"""
Calcola la inversa attraverso l'algoritmo DCT II.
returns: Wave
"""
N = len(self.hs)
ys = scipy.fftpack.idct(self.hs, type=2) / 2 / N
# NOTA: Il primo tempo viene perso nella trasformata
# ts = self.start + np.arange(len(ys)) / self.framerate
return Wave(ys, framerate=self.framerate)
Aggiungiamo il metodo a Wave.
class Wave:
"""
Rappresenta una forma d'onda generica discreta
"""
def __init__(self, ys, ts=None, framerate=None):
"""
ys: collezione di campioni (valori y)
ts: collezione di frames (valori x)
framerate: rata di campionamento
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
return len(self.ys) / self.framerate
def __add__(self, other):
"""Somma due wave campione per campione.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n)
ts = start + np.arange(n) / self.framerate
def add_ys(wave):
i = find_index(wave.start, ts)
diff = ts[i] - wave.start
dt = 1 / wave.framerate
if (diff / dt) > 0.1:
warnings.warn(
"Non posso sommare; il loro " "tempo non coincide."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
def plot(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def plot_vlines(self,curva="linear",**kvargs):
plt.ylim([-1, 1])
plt.yticks([-1,0,1])
plt.grid(True)
#plt.tight_layout()
plt.xscale(curva)
plt.yscale(curva)
plt.vlines(self.ts, 0, self.ys)
plt.plot(self.ts, np.real(self.ys), **kvargs)
def shift(self, shift):
self.ts += shift
def roll(self, roll):
self.ys = np.roll(self.ys, roll)
def truncate(self, n):
self.ys = self.ys[:n]
self.ts = self.ts[:n]
def zero_pad(self, n):
self.ys = zero_pad(self.ys, n)
self.ts = self.start + np.arange(n) / self.framerate
def quantize(self, bound, dtype):
return quantize(self.ys, bound, dtype)
def normalize(self, amp=1.0):
self.ys = normalize(self.ys, amp=amp)
def write(self, filename="sound.wav"):
print("Writing", filename)
wfile = WavFileWriter(filename, self.framerate)
wfile.write(self)
wfile.close()
def play(self, filename="sound.wav"):
self.write(filename)
play_wave(filename)
def make_audio(self):
audio = Audio(data=self.ys.real, rate=self.framerate)
return audio
def copy(self):
return copy.deepcopy(self)
def find_index(self, t):
n = len(self)
start = self.start
end = self.end
i = round((n - 1) * (t - start) / (end - start))
return int(i)
def segment(self, start=None, duration=None):
if start is None:
start = self.ts[0]
i = 0
else:
i = self.find_index(start)
j = None if duration is None else self.find_index(start + duration)
return self.slice(i, j)
def slice(self, i, j):
ys = self.ys[i:j].copy()
ts = self.ts[i:j].copy()
return Wave(ys, ts, self.framerate)
def scale(self, factor):
self.ys *= factor
def window(self, window):
self.ys *= window
def hamming(self):
self.ys *= np.hamming(len(self.ys))
def make_spectrum(self, full=False):
n = len(self.ys)
d = 1 / self.framerate
if full:
hs = np.fft.fft(self.ys)
fs = np.fft.fftfreq(n, d)
else:
hs = np.fft.rfft(self.ys)
fs = np.fft.rfftfreq(n, d)
return Spectrum(hs, fs, self.framerate, full)
def make_sonogram(self, wsize, win_flag=True):
if win_flag:
window = np.hamming(wsize)
i, j = 0, wsize
step = int(wsize // 2)
spec_map = {}
while j < len(self.ys):
segment = self.slice(i, j)
if win_flag:
segment.window(window)
t = (segment.start + segment.end) / 2
spec_map[t] = segment.make_spectrum()
i += step
j += step
return Sonogram(spec_map, wsize)
def unbias(self):
self.ys = unbias(self.ys)
def corr(self, other):
corr = np.corrcoef(self.ys, other.ys)[0, 1]
return corr
def make_dct(self):
"""
Calcola la DCT.
"""
N = len(self.ys)
hs = scipy.fftpack.dct(self.ys, type=2) # Ampiezze
fs = (0.5 + np.arange(N)) / 2 # Frequenze
return Dct(hs, fs, self.framerate)
Verifichiamo.
sig = pym.TriangleSignal(freq=488)
wave = sig.make_wave(duration=1.0,framerate=11050)
dct = wave.make_dct()
dct.plot(high=5000,y_lim=[0,11050],soglia=0.3)
print(dct.hs)
[-5.98077143e-13 2.00000206e+00 1.09164952e-12 ... -4.58783449e-03 2.36828443e-07 -2.04205068e-03]
I valori risultanti dell'analisi dct possono essere sia positivi che negativi.
Nel secondo caso corrispondono a coseni shiftati di 180°.
Esercizi 6Indice
Una delle principali applicazioni della DTC è la compressione di dati sia per l'audio che per il video. Nella forma più semplice segue i seguenti passaggi.
- Frammenta un segnale in segmenti.
- Calcola la DTC per ogni segmento.
- Identifica le frequenze con ampiezza prossima allo zero che sono quasi inudibili e le rimuove salvando solo le rimanenti (minor numero di dati).
- Realizza il playback computando la DFT inversa per ogni segmento.
Implementare una versione di questo algoritmo da applicare su una registrazione musicale o di voce parlata.
Quante frequenze riusciamo a tagliare prima che la differenza sia percepibile?
Per realizzarlo può essere utile approfondire gli sparse array della libreria scipy.
Trasformata discreta di Fourier (DFT)Indice
Il processo è simile a quello illustrato per la DTC.
La sola differenza è data dall'utilizzo della funzione esponenziale complessa al posto della funzione dei coseni.
Per comprenderlo seguiamo gli stessi passi:
Sintesi - definiamo dei parziali attraverso due insiemi uno per le frequenze e uno per le ampiezze. Come possiamo costruire una forma d'onda partendo da questi dati? Questo passo corrisponde alla DFT inversa (IDFT).
Risolviamo il problema del punto precedente attraverso un metodo alternativo e più performante impiegando numpy array.
Analisi - definito un segnale come possiamo trovare le ampiezze e l'offset di fase per ogni frequenza dello spettro?
Risolviamo il problema del punto precedente impiegando l'algebra linerare per migliorare l'efficenza di calcolo.
L'ora di matematicaIndice
Possiamo descrivere il suono in molteplici modi.
Attraverso una partitura musicale, attraverso un qualche tipo di visualizzazione (oscillogramma, spettrogramma, etc.), attraverso una notazione alfabetica (i nomi delle note), oppure attraverso il linguaggio simbolico della matematica essendo il suono un fenomeno fisico appartenente alla realtà.
Questo perchè la matematica ci permette di spiegare concetti e fenomeni del mondo reale sotto forma di generalizzazioni simboliche sulle quali possiamo effettuare operazioni di diverso tipo.
Scopriamo alcuni concetti matematici utili alla piena comprensione dei fenomeni sonori.
Numeri reali - Insieme $\mathbb{R}$ Indice
Ogni numero che può essere rappresentato su una linea retta e con almeno una rappresentazione decimale.
Possono avere:
- la parte decimale limitata o illimitata periodica (numeri razionali - $\mathbb{Q}$ ). Tutti i numeri esprimibili come frazione il cui nominatore e denominatore sono numeri interi ( $1, -2, 0.3, {1 \over 3}, 12.\bar{7}$ ). I numeri razionali contengono anche:
- l'insieme dei numeri interi relativi ($\mathbb{Z}$) il quale contiene a sua volta
- l'insieme dei numeri naturali ($\mathbb{N}$).
- la parte decimale illimitata non periodica (numeri irrazionali). Tutti i numeri che non possono essere espressi come frazione il cui nominatore e denominatore sono numeri interi$\mathbb{I}$ ) ( $-\sqrt{2}, e, \pi, \sqrt{5}$ ).
Il tutto riassunto nel diagramma di Eulero-Venn.
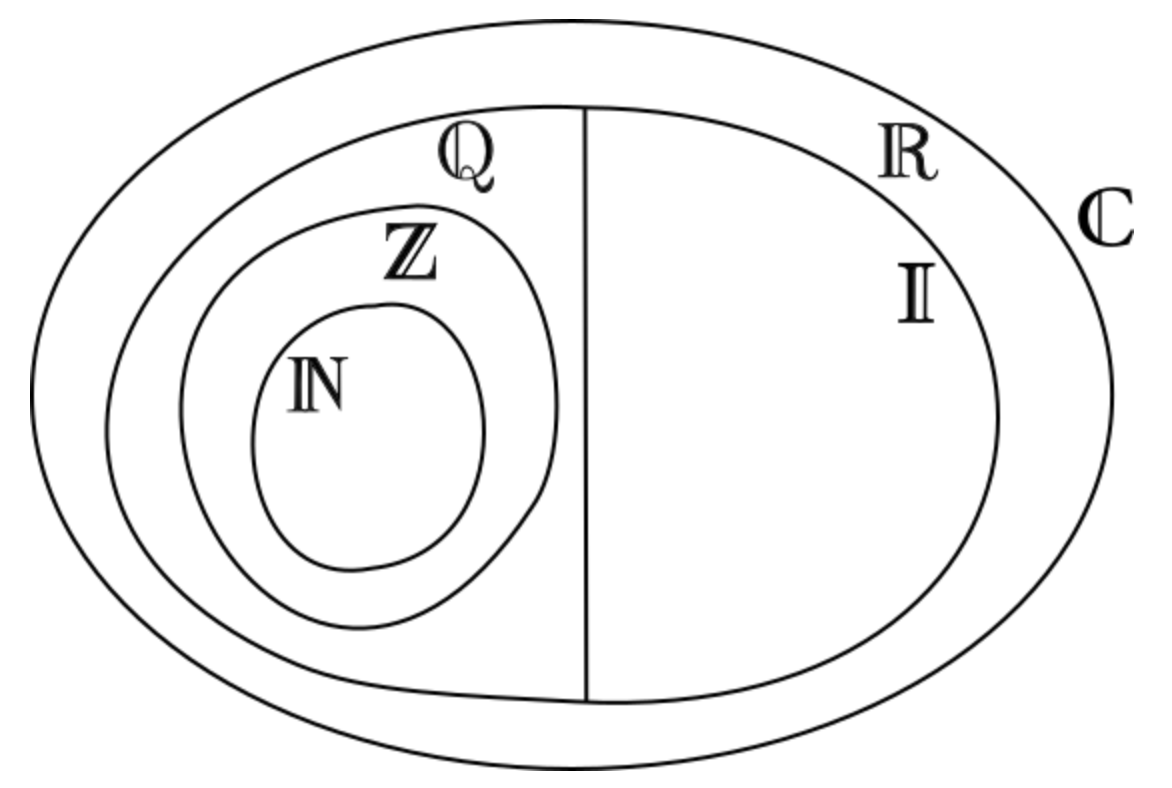
Sommatoria Indice
Sappiamo che lo spettro di un suono è composto da parziali ognuno con una propria frequenza, fase e ampiezza.
Se pizzichiamo al centro una corda bloccata alle sue estremità di lunghezza $L$ comincia a vibrare a una frequenza $f$.
La corda però vibra anche alla metà della sua lunghezza ($\frac{L}{2}$) a una frequenza doppia rispetto a $L$ ($2f$), a un terzo ($\frac{L}{3} - 3f$) e così via fino teoricamente a infiniti segmenti.
Il suono di quella corda è dato dalla somma di tutte queste vibrazioni.
Possiamo generalizzare le caratteristiche di questo fenomeno fisico e descriverle attraverso la matematica.
$$L + \frac{L}{2} + \frac{L}{3} + \frac{L}{4} + \frac{L}{5}... = \sum_{n=1}^{\infty}\frac{L}{n} $$dove il simbolo $\sum$ è chiamato sommatoria.
L = 1 # Lunghezza
n = np.array([L, L/2, L/3, L/4, L/5]) # Rapporti
s = sum(n) # Sommatoria in python
print(s)
2.283333333333333
Un altra caratteristica della matematica è quella secondo la quale possiamo esprimere lo stesso concetto in modi diversi sottolineandone vari aspetti.
Ad esempio possiamo riscrivere l'espressione precedente che descrive a legge armonica nei seguenti modi.
$$\sum_{n=1}^{\infty}\frac{L}{n} = \sum_{n=1}^{\infty}\frac{x}{n}$$Dove $x$ generalizza la lunghezza e se $x = 1 = L$ (unità) possiamo riscriverla in questa forma:
$$\sum_{n=1}^{\infty}\frac{x}{n} = \sum_{n=1}^{\infty}\frac{1}{n}x^n$$x = 1 # Lunghezza
n = 1 # n = 1
p = 1/n * x**n # Polinomio
print(p)
print("-----------")
# Per valori diversi di n
x = 1
n = np.array([1,2,3,4,5]) # Diversi valori di n (incrementali)
p = 1 / n * x**n # Valore a ogni n
print(n)
print(p)
print("-----------")
p = sum(p) # Sommatoria
print(p)
1.0 ----------- [1 2 3 4 5] [1. 0.5 0.33333333 0.25 0.2 ] ----------- 2.283333333333333
a questo punto se sostituiamo il risultato di $\frac{1}{n}$ con $a_n$ la stessa equazione può essere riscritta come:
$$\sum_{n=1}^{\infty}\frac{1}{n}x^n = \sum_{n=1}^{\infty}a_nx^n$$Quest'ultima forma matematica si chiama polinomio.
Polinomi e fattoriali Indice
I polinomi sono importanti quando vogliamo descrivere segnali (audio e non) in quanto speciali tipi di una variabile e composti da una somma di termini di grado crescente moltiplicati da coefficienti.
$$p(x) = a_{0}x^0 + a_{1}x^1 + a_{2}x^2 + a_{3}x^3 + ... + a_{n}x^n = \sum_{n=1}^{\infty}a_nx^n$$n = np.array([1, 2, 3, 4, 5]) # Rapporti (n)
x = 1 # Variabile
a = 1 / n
a = a * x**n # Singolo valore
print(a)
p = sum(a) # Sommatoria
print(p)
[1. 0.5 0.33333333 0.25 0.2 ] 2.283333333333333
Possiamo semplificare i polinomi attraverso la fattorializzazione.
Un fattoriale $n$ ( si scrive !n ) è dato dal prodotto di tutti i numeri interi da $1$ a $n$ e se vogliamo calcolarlo:
$$5! = 5*4*3*2*1 = 120$$x = scipy.special.factorial(5) # Libreria scipy
print(x)
120.0
Un polinomio costituito dalla somma di $n$ termini con grado crescente (esponente), si può scomporre come moltiplicazione di $n$ termini di primo grado.
$$(x^2 - 1) = (x+1)(x-1)$$x = 23 # Valore
a = x**2 - 1 # Polinomio di secondo grado
b = (x+1) * (x-1) # Polinomio di primo grado
print(a, "=", b)
528 = 528
Possiamo allora scomporre il polinomio precedente in questo modo:
$$p(x) = \sum_{n=0}^{\infty}a_nx^n = a_{0}x^0 + a_{1}x^1 + a_{2}x^2 + a_{3}x^3 + ... + a_{n}x^n$$$$p(x) = \sum_{n=0}^{\infty}a_nx^n = (x-b_{0})(x-b_{1})(x-b_{2})(x-b_{3})...(x-b_{n}) = \prod_{n=0}^{n}(x-b_{n})$$Dove il simpbolo $\prod$ sta per produttoria.
La variabile (coefficente) $a_{n}$ della sommatoria è sostutuita dal valore di $b_{n}$ il cui calcolo è complesso ed esula dagli argomenti della presente.
Numero di Nepero Indice
Il numero di Nepero (numero di Eulero) è una costante matematica come il $\pi$ il cui valore è un numero irrazionale ed è indicato come $e = 2.718281...$.
Può essere descritto da un polinomio.
$$e = e^1 = 1 + \frac{1}{1!} + \frac{2}{2!} + \frac{3}{3!} + ...= 2.718281...$$Può essere generalizzato impiegando qualsiasi esponente.
$$e^X = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + ...= 1 + \sum_{n=1}^{\infty}\frac{x^n}{n!}$$x = 1
n = np.array([1,2,3,4,5])
d = scipy.special.factorial(n) # Denominatore (fattoriale)
n = x**n # Numeratore (esponente)
e = n/d
e = 1 + sum(e)
print(e)
2.716666666666667
Lo impiegheremo più avanti sempre rappresentato con la lettera $e$.
Angoli e lati Indice
La trigonometria studia i rapporti tra angoli, cateti e ipotenusa in un triangolo rettangolo.
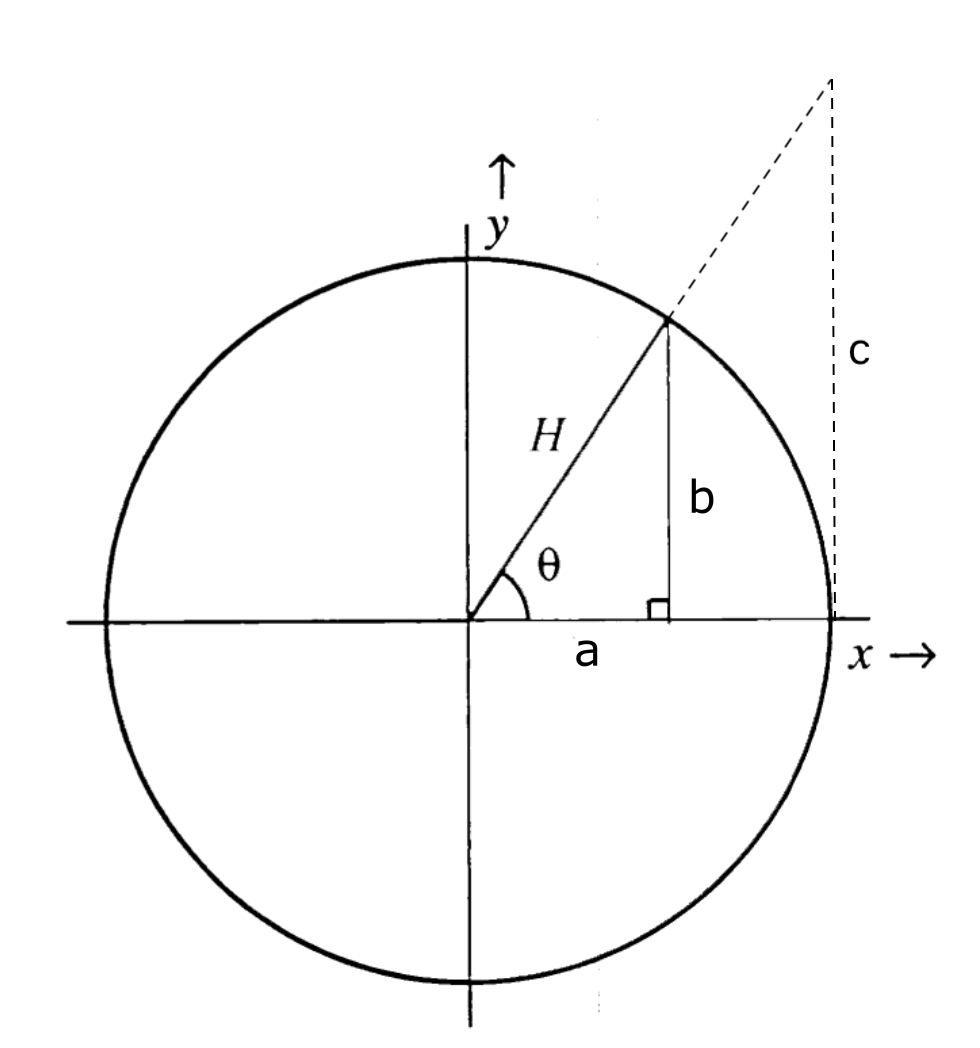
Una sinusoide è definita da:
$$cos(\theta) = ax$$$$sin(\theta) = by$$$$tan(\theta) = c$$Dove $\theta$ (theta) definisce l'angolo con l'asse $x$ positivo (0).
Gli angoli possono espressi in radianti che vanno da $0$ a $2\pi$.

Oppure in gradi che vanno da $0°$ a $360°$ (angolo giro).
Numeri complessi - Insieme $\mathbb{C}$Indice
Un numero complesso è una coppia ordinata di numeri reali e in generale si definisce con la lettera $z$.
$$z = (a,b)$$dove $a$ è detto parte reale mentre $b$ parte immaginaria.
Possiamo considerarlo come un punto su un particolare piano cartesiano chiamato piano complesso.
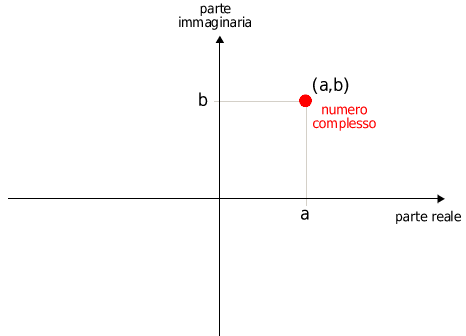
Possiamo rappresentarlo anche in forma algebrica:
$$z = a + i*b$$- $a$ - parte reale
- $i*b$ - parte immaginaria suddivisa in
- $i$ oppure $j$ - unità immaginaria.
- $b$ coefficente reale dell'unità immaginaria.
Possiamo rappresentare anche $a$ e $b$ sotto forma di numeri complessi se le coppie di numeri hanno una coordinata nulla.
- $a = (a,0)$ - numeri reali.
- $b = (0,b)$ - numeri immaginari puri.
L'unità immaginaria $i$ o $j$ è un numero immaginario puro che si identifica con la coppia ordinata:
- $i = (0,1)$
A questo punto l'espressione diventa:
$$z = (a,0) + (0,1) * (0,b)$$Somma e prodotto di numeri complessi si definiscono secondo le seguenti proprietà:
$$(a,b) + (c,d) \iff (a+c, b+d)$$$$(a,b) * (c,d) \iff (ac - bd, ad + bc)$$A questo punto verifichiamo come passare da una forma all'altra con un esempio.
Definiamo $a$ e $b$ con $a=2$ e $b=3$
$$ z = (a, b) \iff (2, 3)$$Rappresentiamo i numeri reali come numeri complessi:
$$z = (a, b) \iff (2, 0) + (0, 3)$$Sotto forma di numeri complessi possiamo scomporre la parte immaginaria $(0,3)$ nel seguente modo:
$$(0,3) = (0,1)*(3,0)$$Riscriviamo la parte immaginaria nella nuova forma:
$$z = (a, b) \iff (2, 0) + (0,1)*(3,0)$$Sapendo che $i = (0,1)$ semplifichiamo:
$$z = (a, b) \iff (2, 0) + i *(3,0)$$Essendoci coordinate nulle nelle coppie ordinate semplifichiamo ulteriormente rappresentando i numeri complessi sotto forma di numeri reali ottenendo la forma algebrica
$$z = (a, b) \iff 2 + i * 3$$Se consideriamo $a = x$ e $b=y$ possiamo rappresentare anche in questo caso il risultato sul piano complesso):
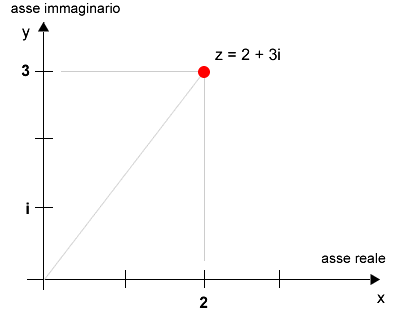
Il calcolo opposto...
z = a + i * b # forma algebrica
z = (a,0) + (0, 1) * (0, b)
z = (a,0) + (0*b − 1*0, 0*0 + 1*b)
z = (a,0) + (0 − 0, 0 + b)
z = (a,0) + (0, b)
z = (a+0, 0+b)
z = (a, b) # numero complesso
I numeri complessi ci permettono di compiere operazioni altrimenti impossibili con i soli numeri reali come:
$$x^2 = -1$$Questo polinomio di secondo grado non ha soluzione in quanto il quadrato (esponente pari) di un qualsiasi numero reale dà sempre un valore positivo e non si può estrarre la radice quadrata di un valore negativo.
Ma...osserviamo una proprietà della moltiplicazione tra numeri complessi applicata all'unità immaginaria.
$$x^2 \iff i^2 \iff i*i \iff (0,1) * (0,1)$$Svolgendo l'operazione la coppia $(0,1)$ se moltiplicata per se stessa (quadrato) ha come risultato l'opposto:
$$(0,1) * (0,1) = (0*0-1*1, 0*1 + 1*0) = (-1, 0) = -1$$Possiamo dunque scrivere:
$$i^2 = -1 \iff x^2 = -1$$risolvendo la prima equazione.
$$i = \sqrt{i^2} = \sqrt{-1}$$che definisce il valore dell'unità immaginaria:
$$i := \sqrt{-1}$$:= significa uguale per definizione.
Questo ci permette di risolvere un'equazioni di secondo grado come la seguente.
$$x^2 + 1 = 0 \iff x^2 = -1 \iff x = \pm{\sqrt{-1}} \iff x = \pm{i}$$Cartesio ha chiamato il valore $\sqrt{-1}$ unità immaginaria in quanto non possiamo rappresentarlo su una retta.
Funzione esponenziale e identità di Eulero Indice
Cominciamo con il ricordare che la definizione di esponente è data da ripetute moltiplicazioni.
$$\phi^3 = \phi * \phi * \phi$$Dove $\phi$ (phi) definisce una funzione d'onda al posto della variabile $x$.
Non possiamo però utilizzare esponenti non interi e quindi generalizzarla.
Possiamo però esprimerla anche come serie di quadrati.
$$e^\phi = 1+\frac{\phi}{1!} + \frac{\phi^2}{2!} + \frac{\phi^3}{3!} + \frac{\phi^4}{4!} + ... $$Che coincide con il polinomio impiegato per generalizzare il numero di Nepero ($e$).
Questa definizione è valida anche per i numeri complessi introducendo l'unità immaginaria.
$$e^{i\phi} = 1 + \frac{i\phi}{1!} + \frac{(i\phi)^2}{2!} + \frac{(i\phi^3)}{3!} + \frac{(i\phi^4)}{4!} + ... $$Possiamo rappresentare anche $sin$ e $cos$ in forma polinomiale come risultato di uno sviluppo in serie di Taylor.
$$sin(\theta) = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + ...$$$$cos(\theta) = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \frac{\theta^6}{6!} + ...$$Ricordiamo che $\theta$ (theta) definisce l'angolo con l'asse delle $x$.
Esiste una formula che mette in relazione il numero di Neplero con $sin$ e $cos$ attraverso una rappresentazione polinomiale.
Se $i^2 = -1$ come dimostrato pocanzi:
$$e^{i\phi} = 1 + \frac{i\phi}{1!} + \frac{(i\phi)^2}{2!} + \frac{(i\phi^3)}{3!} + \frac{(i\phi^4)}{4!} + ... $$$$= \biggl[1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \frac{\theta^6}{6!} + ... \biggr] + i\biggl[\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + ... \biggr]$$$$= cos(\theta) + i \ sin(\theta)$$Questa equazione è conosciuta come formula di Eulero e si basa sulla funzione esponenziale di un numero complesso.
$$e^{z} = cos(\theta) + i \ sin(\theta)$$A questo punto possiamo affermare che un numero complesso può essere rappresentato in tre forme:
- forma cartesiana (x y): $z = a + ib $
- forma trigonometrica: $H(cos(\theta) + i \ sin(\theta))$
- forma esponenziale: $H \cdot e^{i\phi}$
Dove $H$ è il raggio di una cisconferenza.
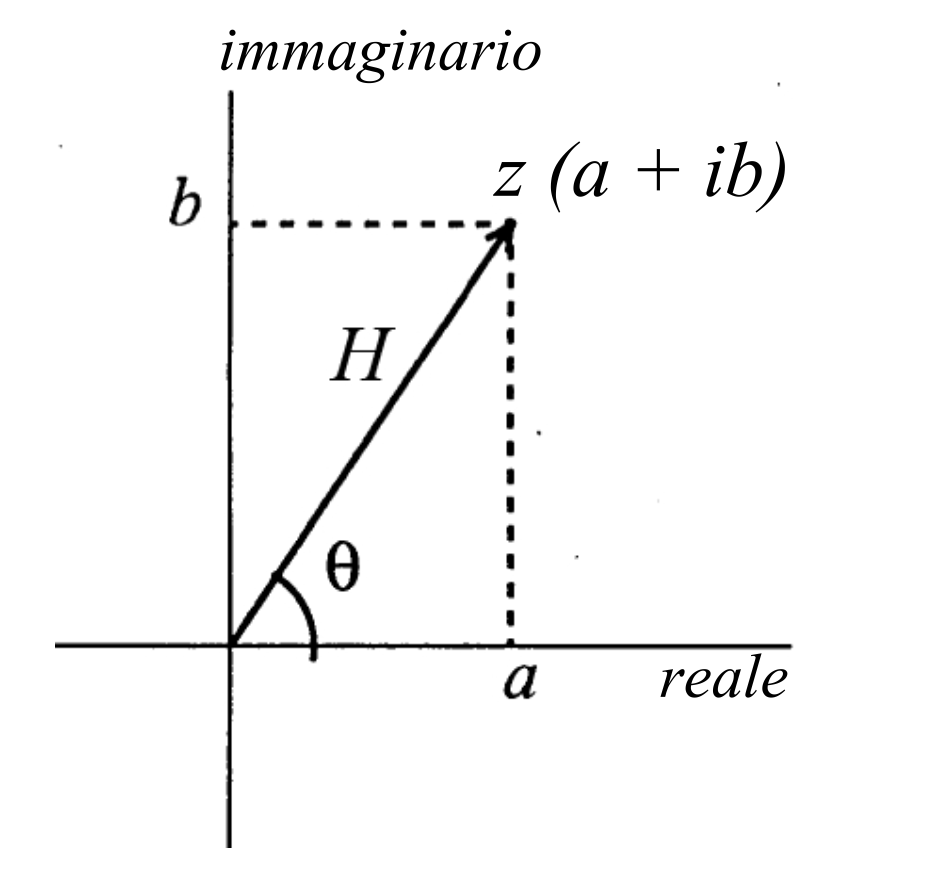
Numeri complessi in Python Indice
La formula di Eulero implica che $e^{z}$ sia un numero complesso con magnitudine 1.
Se lo pensiamo nel piano complesso è sempre sulla circonferenza con raggio = 1.
L'angolo in radianti corrisponde al valore di $\phi$ (phi).
In quanto numero complesso possiamo rappresentare $z$ in questa forma:
$$e^{a\ +\ i\phi} = e^ae^{i\phi} = Ae^{i\phi}$$Dove $A$ è un numero reale che indica l'ampiezza mentre $e^{i\phi}$ è un numero complesso che indica l'angolo (fase).
In numpy possiamo calcolare il valore di $e^{i\phi}$ (numero di Nepero) con exp() specificando un esponente sia reale che complesso.
phi = 1.5 # Angolo in radianti (da 0 a 2pi)
z = np.exp(1j * phi) # Esponente complesso
print(z)
(0.0707372016677029+0.9974949866040544j)
In Python l'unità immaginaria è rappresentata con j.
I numeri complessi sono sotto la forma di np.complex128 che è formato da due numeri decimali a 64-bit.
Possiamo estrarre la parte reale e quella immaginaria.
print(z.real)
print(z.imag) # Approssimata...
0.0707372016677029 0.9974949866040544
Possiamo ottenere la magnitudine e/o l'angolo.
print(np.absolute(z)) # Magnitudine
print(np.angle(z)) # Angolo (in radianti)
1.0 1.5
Segnali complessiIndice
Se $\phi(t)$ è una funzione che calcola la fase (ampiezza istantanea) nel tempo lo è anche $e^{i\phi(t)}$ o meglio:
$$e^{i\phi(t)} = cos(\theta(t)) + i \ sin(\theta(t))$$Siccome questa descrive una quantità che varia nel tempo possiamo dire che è un segnale e nello specifico un segnale esponenziale complesso.
Se la frequenza è costante il risultato è una sinusoide complessa.
$$e^{i2\pi ft} = cos(2\pi ft) + i \ sin(2\pi ft)$$O più generalmente:
$$e^{i(2\pi ft + \phi_{0})}$$Ricordiamo che la funzione d'onda nel dominio del tempo di un' onda sinusoidale è:
$$y_{(t)} = A * sin(\omega t+\phi_{0})$$Dove $\omega = 2\pi f$ (velocità angolare).
Implementiamo una classe per questo segnale che eredita il costruttore da Sinusoid.
class ComplexSinusoid(Sinusoid):
"""Rappresenta un segnale complesso esponenziale."""
def evaluate(self, ts):
"""Valuta una funzione a tempi discreti.
ts: float array do onsets
returns: float wave array
"""
ts = np.asarray(ts) # Array di onsets
phases = PI2 * self.freq * ts + self.offset # 2pift+0
ys = self.amp * np.exp(1j * phases) # e^2pift+0
return ys
sig = pym.ComplexSinusoid(freq=1,amp=0.6,offset=1)
wave = sig.make_wave(duration=1.0,framerate=4)
print(wave.ys) # valori y
[ 0.32418138+0.50488259j -0.50488259+0.32418138j -0.32418138-0.50488259j 0.50488259-0.32418138j]
Il risultato è un array di numeri complessi (quattro valori tra 0 e 1).
SintesiIndice
Coma abbiamo già fatto con sinusoidi reali possiamo sommare tra loro sinusoidi complesse ognuna con una propria frequenza e ampiezza.
Il modo più semplice consiste nel sommare tra loro più istanze di ComplexSinusoid come abbiamo già fatto per la DTC
def sintesi1_dft(amps, fs, ts):
componenti = [pym.ComplexSinusoid(freq, amp) # Parziali complessi
for amp, freq in zip(amps, fs)] # zip() crea una tuple da elementi di due array diversi
signal = pym.SumSignal(*componenti) # * = numero indefinito di attributi
ys = signal.evaluate(ts)
return ys
amps = np.array([0.6, 0.25,0.1, 0.05]) # Somma deve dare 1.0
fs = [100, 200, 300, 400]
framerate = 11025
ts = np.linspace(0,1,framerate) # Array di onsets - definisce la durata (1 secondo)
ys = sintesi1_dft(amps, fs, ts) # Genera l'array di ampiezze istantanee
print(ys)
[1. +0.00000000e+00j 0.99465119+9.09309464e-02j 0.97873848+1.80300718e-01j ... 0.97873848-1.80300718e-01j 0.99465119-9.09309464e-02j 1. -5.08264626e-15j]
Il risultato è una sequenza di numeri complessi ovvero un segnale complesso.
Ma cos'è un segnale complesso?
Ci sono due possibili risposte non del tutto soddisfacenti.
Un segnale complesso è un'astrazione matematica utile per il calcolo e l'analisi ma che non ha nulla a che fare con il mondo reale.
Un segnale complesso può essere pensato come sequenza di numeri complessi che contengono due segnali uno come parte reale e l'altro come parte immaginaria.
Partendo da questo secondo punto di vista possiamo splittare le due parti e visualizzarle in un plot.
n = 500
plt.plot(ts[:n], ys[:n].real, label='reale')
plt.plot(ts[:n], ys[:n].imag, label='immaginaria')
plt.legend()
<matplotlib.legend.Legend at 0x153951e90>
Osserviamo che la parte reale è una somma di coseni mentre la parte immaginaria una somma di seni e, nonostante le forma d'onda sembrino differenti hanno le stesse componenti frequenziali e alle nostre orecchie suonerebbero identiche.
Sintesi con np.array (matrici)
Esattamente come abbiamo fatto per la DTC possiamo realizzare la sintesi attraverso la moltiplicazione di matrici.
def sintesi2_dft(amps, fs, ts):
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.exp(1j * PI2 * args) # funzione esponenziale al posto dei coseni
ys = np.dot(M, amps) # riscala le ampiezze
return ys # campioni
La funzione precedente è identica a quella illustrata per la DTC ad eccezione di M.
Questo perchè nella DTC le ampiezze sono espresse attraverso numeri reali mentre in questo caso in numeri complessi.
Ricordiamo che possiamo pensare i numeri complessi sia come somma di parte reale e immaginaria $x + iy$ che come il prodotto di un'ampiezza reale e un esponente complesso $Ae^{i\phi_0}$.
Impiegando la seconda formula osserviamo cosa succede se moltiplichiamo un ampiezza complessa per una sinusoide complessa.
$$Ae^{i\phi_0} \cdot e^{i2\pi ft} = Ae^{i2\pi ft \ + \ \phi_0} $$amps = np.array([0.6, 0.25,0.1, 0.05]) # Ampiezze reali
fs = [100, 200, 300, 400] # Frequenze
ts = np.linspace(0,1,framerate) # Onsets (1 secondo)
phi = 1.5 # Fase iniziale
amps2 = amps * np.exp(1j * phi) # Ampiezze complesse sfasate di phi
ys = sintesi2_dft(amps, fs, ts) # ys reali
ys2 = sintesi2_dft(amps2, fs, ts) # ys complessi
n = 500
plt.plot(ts[:n], ys[:n].real, label='fase=0')
plt.plot(ts[:n], ys2[:n].real, label='fase=' + str(phi))
plt.legend()
<matplotlib.legend.Legend at 0x154040d90>
Le forme d'onda hanno aspetto differente perchè sfasando di 1.5 significa spostarla di mezzo ciclo e il ciclo di ogni parziale è differente a causa della diversa frequenza.
AnalisiIndice
Data sequenza di ampiezze istantanee (ys) e di frequenze dei parziali (fs) come possiamo calcolarne le ampiezze complesse (amps2)?
Come nel caso della DTC possiamo risolvere questo problema attraverso la risoluzione di un sistema lineare $Ma = y$ modificando M come per la sintesi.
def analisi1(ys, fs, ts): # DTC
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.cos(PI2 * args) # cos(2pi*f*t)
amps = np.linalg.solve(M, ys) # calcola le ampiezze
return amps
def analisi1_dft(ys, fs, ts): # DFT
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.exp(1j * PI2 * args) # funzione esponenziale al posto dei coseni
amps = np.linalg.solve(M, ys) # calcola le ampiezze
return amps
Per i sistemi lineari ricordiamo che i vettori ys, fs e ts devono avere lo stesso numero di elementi
amps = np.array([0.4, 0.25, 0.1, 0.05, 0.2])
fs = [200, 300, 400, 500, 600]
framerate = 11025
ts = np.linspace(0,1,framerate)
ys = sintesi1_dft(amps, fs, ts) # ----------> Sintesi
n = len(fs) # Numero di frequenze (bins)
a = analisi1_dft(ys[:n], fs[:n], ts[:n]) # ----------> Analisi
# Tutti gli arrays hanno la stessa lunghezza
print(a)
[0.4 +1.10458864e-12j 0.25-4.52054019e-12j 0.1 +6.85671658e-12j 0.05-4.57006655e-12j 0.2 +1.12944376e-12j]
Verifichiamo in questo modo che le ampiezze complesse ottenute dall'analisi sono quasi uguali a quelle impiegate per la sintesi con la sola differenza di una piccola parte immaginaria dovuta all'approssimazione decimale.
Per ottimizzare la computazione, nella DTC abbiamo scelto il numero di fs e di ts affinchè la matrice $M$ fosse ortogonale ($M^{T}$) ovvero le righe diventano colonne e viceversa (dove T è la sua matrice trasposta).
Possiamo fare la stessa cosa per la DFT con una piccola differenza.
Siccome $M$ è una matrice complessa abbiamo bisogno che sia una matrice unitaria invece che ortogonale ovvero che l'inverso di $M$ sia il coniugato trasposto di $M$ che possiamo calcolare trasponendo la matrice e rendendo negativa la parte immaginaria di ogni elemento.
I metodi transpose e conj di NumPy effettuano queste operazioni.
Esempio con 4 componenti.
n = 4
ts = np.arange(n) / n # Frames
fs = np.arange(n) # Frequenze
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.exp(1j * PI2 * args) # funzione esponenziale
Se $M$ è una matrice unitaria, $M°M = I$ dove $M°$ è il coniugato trasposto di $M$ e $I$ è la matrice d'identità (1.0 sulla diagonale).
Possiamo verificare se $M$ è unitaria in questo modo.
MoM = M.conj().transpose().dot(M)
print(MoM)
[[ 4.00000000e+00+0.00000000e+00j -1.83697020e-16+2.22044605e-16j 0.00000000e+00+2.44929360e-16j 3.29046455e-16+3.33066907e-16j] [-1.83697020e-16-2.22044605e-16j 4.00000000e+00+0.00000000e+00j -1.83697020e-16+2.22044605e-16j 0.00000000e+00+2.44929360e-16j] [ 0.00000000e+00-2.44929360e-16j -1.83697020e-16+0.00000000e+00j 4.00000000e+00+0.00000000e+00j -1.83697020e-16+2.22044605e-16j] [ 3.29046455e-16-3.33066907e-16j 0.00000000e+00-2.44929360e-16j -1.83697020e-16-2.22044605e-16j 4.00000000e+00+0.00000000e+00j]]
Osserviamo che il risultato sulla diagonale al netto degli errori decimali è $4I$ e dunque $M$ in questo caso è unitaria ad eccezione di un fattore di $n$ (4) similmante all'extra fattore di 2 che abbiamo riscontrato nella DTC.
Possiamo ora riscrivere una versione più veloce di analisi1_DFT.
def analisi2_dft(ys, fs, ts): # DFT ottimizzata
args = np.outer(ts,fs) # f*t ad ogni ts
M = np.exp(1j * PI2 * args) # funzione esponenziale al posto dei coseni
amps = M.conj().transpose().dot(ys) / n # MODIFICATO e riscalato dell'extra fattore
return amps
n = 4
amps = np.array([0.6, 0.25, 0.1, 0.05])
fs = np.arange(n)
ts = np.arange(n) / n
ys = sintesi2_dft(amps, fs, ts) # ----------> Sintesi
amps3 = analisi2_dft(ys, fs, ts) # ----------> Analisi
print(amps3)
[0.6 +1.38777878e-17j 0.25+9.18485099e-18j 0.1 -3.46944695e-17j 0.05-8.30657042e-17j]
Notiamo che il risultato dell'analisi è corretto al netto degli errori decimali.
La funzione analisi2_dft però non è molto utile ai fini pratici in quanto funziona solo se scegliamo correttamente frequenze (fs) e frames (ts).
Riscriviamola in modo che accetti solo ampiezze istantanee (ys) ricavando frequenze (fs) e frames (ts) da queste.
Definiamo una funzione che calcola la matrice di sintesi.
def matrice_sintesi(n):
ts = np.arange(n) / n # Fames
fs = np.arange(n) # Frequenze (bins)
args = np.outer(ts, fs) # f*t ad ogni ts
M = np.exp(1j * PI2 * args) # Funzione esponenziale
return M
Definiamo una funzione che accetta ampiezze istantanee (ys) e restituisce le ampiezze di parziali.
def analisi3_dft(ys):
n = len(ys)
M = matrice_sintesi(n)
amps = M.conj().transpose().dot(ys) / n
return amps
La differenza tra questa funzione e la definizione convenzionale di DFT consiste nel fatto che quest'ultima non divide il risultato per $n$ (normalizza).
def dft(ys):
n = len(ys)
M = matrice_sintesi(n)
amps = M.conj().transpose().dot(ys)
return amps
Verifichiamo
n = 4
amps = np.array([0.6, 0.25, 0.1, 0.05])
fs = np.arange(n)
ts = np.arange(n) / n
ys = sintesi2_dft(amps, fs, ts) # ----------> Sintesi
amps3 = dft(ys) # ----------> Analisi
print(amps3)
[2.4+5.55111512e-17j 1. +3.67394040e-17j 0.4-1.38777878e-16j 0.2-3.32262817e-16j]
Il risultato è $amps * n$.
Proviamo a comparare il risultato compiendo la stessa operazione con la funzione dedicata alla fft di NumPy.
amps4 = np.fft.fft(ys)
print(amps4)
[2.4+5.22485116e-17j 1. -2.44929360e-17j 0.4-3.26263963e-18j 0.2-2.44929360e-17j]
Notiamo che è identico al netto degli errori decimali.
DFT inversaIndice
Per calcolare la DFT inversa (IDFT) ovvero ottenere ampiezze istantanee (ys) da frequenze (fs) e ampiezze (amps) dei parziali dobbiamo compiere le stesse operazioni senza calcolare il coniugato trasposto ma dividendo il risultato per $n$.
def idft(ys):
n = len(ys)
M = matrice_sintesi(n)
amps = M.dot(ys) / n
return amps
Verifichiamo
amps = np.array([0.6, 0.25, 0.1, 0.05])
ys = idft(amps) # IDFT
amps5 = dft(ys) # DFT
print(amps5)
[0.6 +1.38777878e-17j 0.25+9.18485099e-18j 0.1 -3.46944695e-17j 0.05-8.30657042e-17j]
DFT di segnali realiIndice
La classe Spectra che abbiamo utilizzato per visualizzare uno spettrogramma è basata sull'oggetto np.fft.rfft di NumPy che computa la DFT reale ovvero effettua i calcoli su segnali descritti attraverso numeri reali.
La DFT appena descritta invece opera su numeri complessi (full DFT).
Cosa succede dunque se calcoliamo una full DFT su un segnale reale?
sig = pym.SquareSignal(500) # Onda quadra
wave = sig.make_wave(0.1, 10000) # durata = 0.1 secondi, framerate = 10000
hs = dft(wave.ys) # DFT complessa
amps = np.absolute(hs) # Ampiezza di ogni parziale
In questo esempio amps contiene l'ampiezza di ogni parziale ma quali sono le frequenze dei parziali?
Se guardiamo all'interno della funzione matrice_sintesi contenuta nella funzione dft() possiamo osservare che:
n = 100
fs = np.arange(n) # Contenuto in matrice_sintesi
print(fs)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99]
Ovvero potremmo pensare che siano queste ma il problema consiste nel fatto che queste funzioni non conoscono la rata di campionamento assumendo che la durata sia 1 unità di tempo e che la rata di campionamento sia $N$ per unità di tempo (ovvero $N-1$).
Per computare correttamente le frequenze dobbiamo convertire questi valori arbitrari in secondi.
n = 100
framerate = 10000
fs = np.arange(n) * framerate / n
print(fs)
[ 0. 100. 200. 300. 400. 500. 600. 700. 800. 900. 1000. 1100. 1200. 1300. 1400. 1500. 1600. 1700. 1800. 1900. 2000. 2100. 2200. 2300. 2400. 2500. 2600. 2700. 2800. 2900. 3000. 3100. 3200. 3300. 3400. 3500. 3600. 3700. 3800. 3900. 4000. 4100. 4200. 4300. 4400. 4500. 4600. 4700. 4800. 4900. 5000. 5100. 5200. 5300. 5400. 5500. 5600. 5700. 5800. 5900. 6000. 6100. 6200. 6300. 6400. 6500. 6600. 6700. 6800. 6900. 7000. 7100. 7200. 7300. 7400. 7500. 7600. 7700. 7800. 7900. 8000. 8100. 8200. 8300. 8400. 8500. 8600. 8700. 8800. 8900. 9000. 9100. 9200. 9300. 9400. 9500. 9600. 9700. 9800. 9900.]
Osserviamo che in questo caso le frequenze vanno da 0 alla rata di campionamento.
Torniamo all'esempio sul segnale reale e realizziamo un plot.
sig = pym.SquareSignal(500) # Onda quadra
framerate = 10000 # Rata di campionamento
wave = sig.make_wave(0.1, framerate) # durata = 0.1 secondi, framerate = 10000
hs = dft(wave.ys) # DFT complessa
amps = np.absolute(hs) # Ampiezza di ogni parziale
n = len(wave.ys) # Numero di campioni (window size)
fs = np.arange(n) * framerate / n # Calcola le frequenze (bins)
plt.plot(fs, amps)
[<matplotlib.lines.Line2D at 0x15406b090>]
Il plot visualizza l'ampiezza di ogni parziale la cui frequenza è compresa tra 0 e 10.000 Hz (la frequenza di campionamento che abbiamo scelto).
Fino a metà (5.000 Hz) visualizziamo quello che ci aspettiamo ovvero le ampiezze decrescono secondo il rapporto $1 / f$ mentre oltre questa soglia cominciano a crescere in modo speculare.
Perchè?
La risposta è: aliasing.
Siccome la DFT di un segnale è simmetrica attorno al limite di Nyquist ovvero frequanza di campionamento / 2 possiamo calcolare solo la prima parte di DFT come fa esattamente np.fft.rfft.
FFT - un esempio praticoIndice
La FFT (Fast Fourier Transform) è un algoritmo che ottimizza la computazione della DFT.
In python abbiamo a disposizione tre modi per computare la FFT di un segnale:
- il modulo numpy.fft - meno completo dell'ultimo in elenco offre una maggiore compatibilità con versioni vecchie di python.
- il modulo scipy.fftpack - una versione obsoleta.
- il modulo scipy.fft - un'ottimizzazione del modulo precedente con API rinnovate da preferire ai due precedenti.
Vediamo come impiegare la FFT in un esempio pratico.
individuiamo e rimuoviamo un suono periodico indesiderato (come il trillo di un telefonino in una registrazione live) da un segnale.
Anche in questo caso stilizziamo semplificando gli elementi.
Generiamo un segnale sinusoidale definendo una funzione (senza utilizzare le classi che abbiamo già definito per ripassare alcuni concetti).
SAMPLE_RATE = 44100 # Hertz
DURATION = 2 # Secondi
def genera_sine(freq, sample_rate, dur):
x = np.linspace(0, dur, sample_rate * dur, endpoint=False)
freqs = x * freq
y = np.sin(PI2 * freqs) # sin(2 * pi * freq)
return x, y
x, y = genera_sine(2, SAMPLE_RATE, DURATION) # Genera un segnale di 5 secondi a 2 Hz
plt.plot(x, y)
plt.show()
Generiamo e sommiamo tra loro due sinusoidi valutando la funzione.
Ognuna rappresenta una parte della registrazione da correggere.
_, musica = genera_sine(400, SAMPLE_RATE, DURATION) # Rappresenta la musica
_, telefono = genera_sine(4000, SAMPLE_RATE, DURATION) # Rappresenta il suono del telefono
telefono = telefono * 0.3 # Riscaliamo l'ampiezza del telefono
tape = musica + telefono # Mix dei due segnali (la registrazione originale)
La funzione restituisce due valori (x, y) l'underscore non prende in considerazione i valori x.
Ora dobbiamo normalizziarle ovvero riscalare le ampiezze affinchè rientrino nel range del formato finale che in questo caso è 16-bit integer che comprende valori tra -32.767 e +32.767 ($\frac{2^{16}}{2}$).
normalizzato = np.int16((tape / tape.max()) * 32767) # prima riscala tra -1 e +1 poi moltiplica
plt.plot(normalizzato[:1000]) # solo i primi 1000 campioni
plt.show()
Audio(data=normalizzato, rate=SAMPLE_RATE) # Audio
Ha l'aspetto di un suono distorto dove la curva principale è data dalla sinusoide a 400Hz mentre il 'disturbo' quella a 4000Hz.
Analizziamolo con l'oggetto scipy.fft e visualizziamo il risultato in uno spettrogramma.
from scipy.fft import fft, fftfreq
N = SAMPLE_RATE * DURATION # Numero di campioni
yf = fft(normalizzato) # Calcola la FFT
xf = fftfreq(N, 1 / SAMPLE_RATE) # Calcola la frequenza al centro di ogni bin
plt.plot(xf, np.abs(yf)) # abs() perchè xf sono numeri complessi
plt.show()
Possiamo notare la presenza di frequenze positive e negative come conseguenza dell'FFT un un segnale reale.
Notiamo anche che fftfreq calcola la frequenza di ogni bins e che la parte positiva arriva a 22.050Hz ovvero la frequenza di Nyquist rispetto alla frequenza di campionamento che abbiamo indicato.
Per la visualizzazione del plot abbiamo dovuto convertire $xs$ da numeri complessi ($a + bj$) a numeri reali con abs() che calcola $\sqrt{(a^2 + b^2)}$ ottenendo un singolo valore medio tra parte reale e parte immaginaria.
Anche in scipy possiamo computare la FFT di un segnale reale con l'oggetto rfft modificando di poco il codice precedente e incrementando la velocità di calcolo.
from scipy.fft import rfft, rfftfreq
yf = rfft(normalizzato)
xf = rfftfreq(N, 1 / SAMPLE_RATE)
plt.plot(xf, np.abs(yf))
plt.show()
Ora possiamo filtrare il segnale eliminando la frequenza a 4.000Hz.
Il fisultato di rfft rappresentano l'ampiezza di ogni frequenza ad ogni bin.
Se cambiamo l'ampiezza della frequenza del telefonino settandola a 0.0 il suono sarà eliminato.
Basterà trovare l'indice del bin corrispondente.
punti_per_freq = len(xf) / (SAMPLE_RATE / 2) # Calcola il delta tra due bins
# La frequenza massima è la metà della rata di campionamento
target_idx = int(punti_per_freq * 4000) # Lo moltiplica per la frequenza desiderata
yf[target_idx - 1:target_idx + 2] = 0 # Setta l'indice e i suoi vicini a 0
plt.plot(xf, np.abs(yf))
plt.show()
Ora possiamo applicare la IFFT ovvero la trasformata reale inversa per ottenere i valori y 'ripuliti' dal sengale originale.
from scipy.fft import irfft
pulito = irfft(yf)
plt.plot(pulito[:1000])
plt.show()
Audio(data=pulito, rate=SAMPLE_RATE)
Nella realtà i filtri FFT non sono come quello appena descritto in quanto se applicato a spettri più ricchi di parziali potrebbero introdurre molti artefatti nel segnale ottenuto (Filtering Pitfalls) ma possiamo considerarlo un esempio didattico.