Home

Parametri degli eventi sonori¶

Indice¶

  • Altezza o frequenza
    • Misurazioni e rappresentazioni
    • Implicazioni musicali
  • Dinamica o ampiezza
    • Misurazioni e rappresentazioni
    • Implicazioni musicali
  • Strumenti o timbro
    • Misurazioni e rappresentazioni
    • Implicazioni musicali
  • Fase e moto armonico
    • Misurazioni e rappresentazioni
    • Implicazioni musicali
  • Disposizione o spazializzazione
  • Tempo e pulsazioni
    • Misurazioni e rappresentazioni
    • Implicazioni musicali

Altezza o frequenza Indice

L’altezza (o frequenza) di un suono è il parametro legato alla sensazione di gravità/acutezza che si percepisce e dipende dalle frequenze di variazione delle onde elementari che compongono l’onda sonora.

Misurazioni e rappresentazioni Indice

Possiamo specificare questo parametro in tre diversi tipi di notazione simbolica:

  1. Simboli musicali - determinano l'altezza in base alla posizione grafica in un contesto di linguaggio codificato (la scrittura musicale). Sono relativi alle regole sintattiche del codice impiegato (se non conosco il codice non posso interpretare l'informazione) ma non necessariamente di quelle del sistema musicale impiegato.
In [1]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Simboli.png" width="40%"></center>')
Out[1]:

  1. Simboli alfabetici - determinano l'altezza come nomi di una scala o un modo. Sono relative alle regole sintattiche (rapporti intervallari) del sistema di regole musicali di riferimento.

    Esempi: Scala di Do maggiore, Scala di Fa minore, Modo frigio, etc.

In [2]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Nomi.png" width="40%"></center>')
Out[2]:

Guido d'Arezzo - Inno a San Giovanni Battista (1028 ca.)

In [3]:
from IPython.display import HTML 
HTML('<center><video width="40%" controls> <source src="media/nomi.mp4"></video></center>')
Out[3]:
  1. Simboli numerici - in questo caso possiamo fare un'ulteriore suddivisione in quattro diverse unità:

  • Gradi - determinano l'altezza come posizioni in una scala o in un modo. Sono relative alle regole musicali (rapporti intervallari) del sistema di riferimento ma non univochi in quanto permettono una trasposizione dinamica del modello intervallare (un I grado può essere un do, oppure un fa, oppure un sol...).

    Esempi: Scala maggiore, Scala per toni interi, Scala pentatonica, etc.

In [4]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Gradi.png" width="40%"></center>')
Out[4]:

  • Rapporti intervallari - determinano l'altezza come distanza da un'altezza di riferimento (root note) in genere definita con il valore 0. L'unità può corrispondere al semitono o a un altro passo di riferimento. Non sono relative alle regole musicali (rapporti intervallari) di alcun sistema di riferimento e non sono univochi in quanto la loro altezza dipende dalla root note.

     do re mi fa sol la si
  0  2  4  5  7   9  11
In [5]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Intervalli.png" width="40%"></center>')
Out[5]:
  • MIDI Note - determinano l'altezza come valori numerici 60 = Do centrale. Non sono relative alle regole musicali (rapporti intervallari) di alcun sistema di riferimento e sono univochi in quanto la loro altezza è assoluta.
In [6]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Midi.png" width="40%"></center>')
Out[6]:

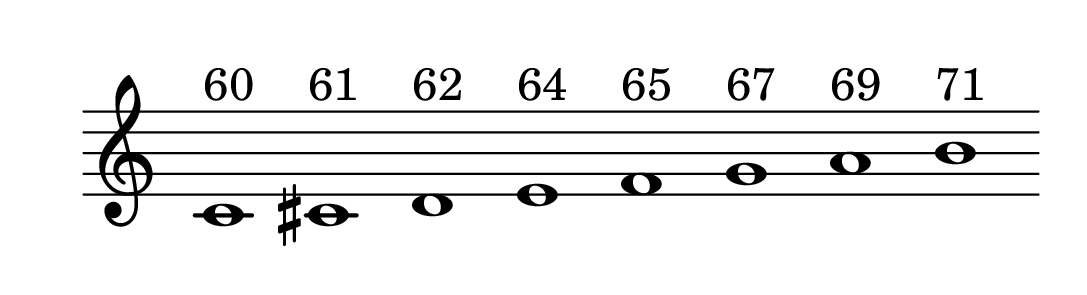
Oltre ai valori midi esistono altre rappresentazioni simboliche assolute impiegate:

  1. Numerazione MIDI.
  2. Numerazione a Ottave (Giapponese, Yamaha, Encore).
  3. Numerazione a Ottave (Scientifica, MusicXML ed altre).
  4. Numerazione di Helmholtz (utilizzata comunemente negli Stati Uniti).
  5. Numerazione Esadecimale.
In [7]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Altezze.png" width="63%"></center>')
Out[7]:
  • Frequenze (Hertz) - determinano l'altezza come valori numerici che rappresentano il numero di cicli per secondo di un'onda periodica o ciclica. Non sono relative alle regole sintattiche (rapporti intervallari) di alcun linguaggio musicale di riferimento e sono univochi in quanto la loro altezza è assoluta.
In [8]:
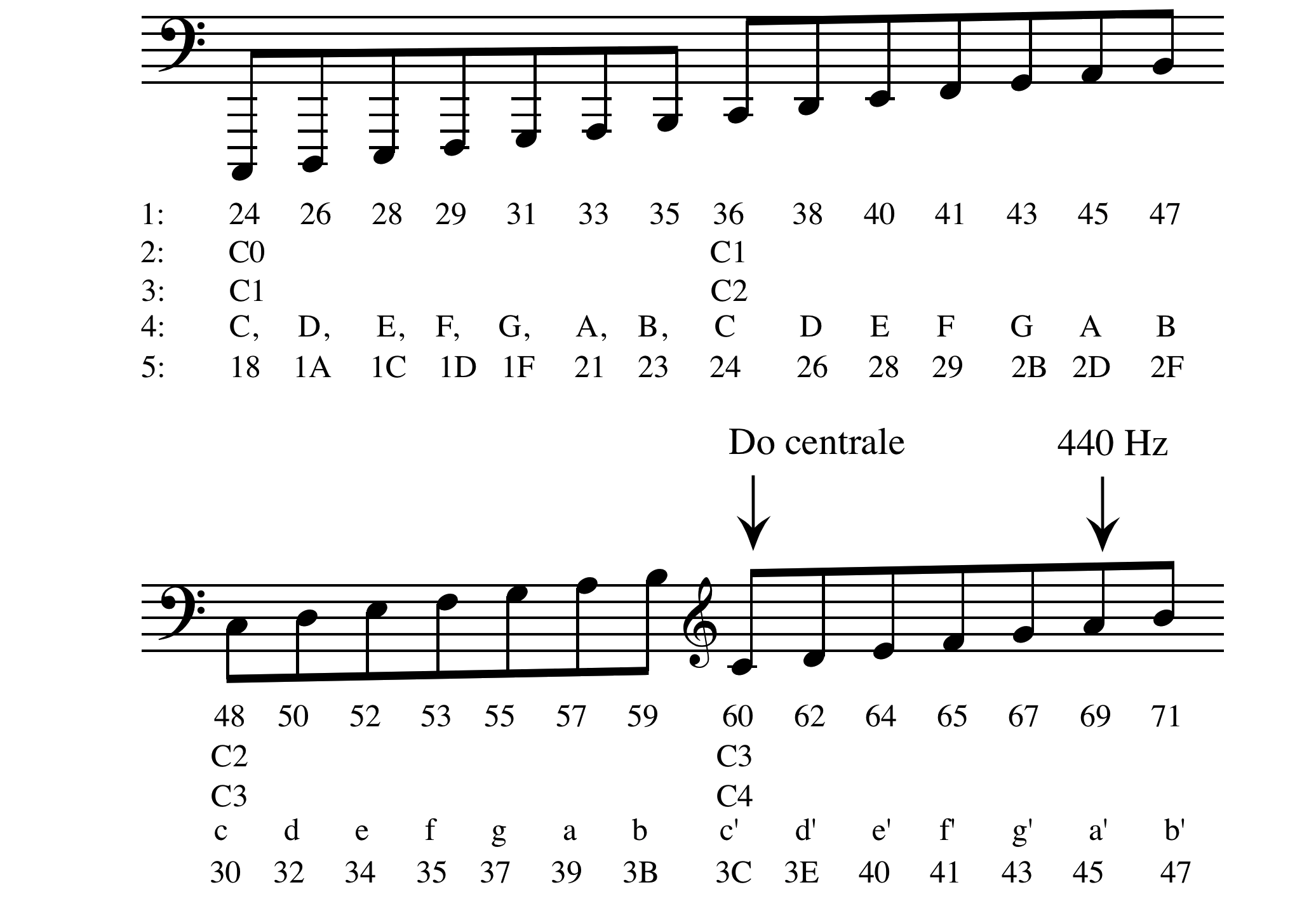
from IPython.display import HTML 
HTML('<center><img src="esempi/Frequenze.png" width="40%"></center>')
Out[8]:

Un'onda periodica è data da un fenomeno vibratorio che si ripete identico a se stesso a intervalli di tempo uguali.

  • se il singolo intervallo viene misurato nel tempo è chiamato periodo (o ciclo) dell'onda e rappresentato dalla lettera T.
  • se il singolo intervallo viene misurato nello spazio è chiamato lunghezza dell'onda e rappresentato dalla lettera $\lambda$ - lambda.

Possiamo rappresentare graficamente un onda attraverso un sistema di riferimento cartesiano:

  • asse delle ascisse (x) = scorrere del tempo
  • asse delle ordinate (y) = variazioni di pressione atmosferica

La frequenza di un suono periodico è misurata in Hertz o cps (cicli per secondo) ovvero si misura quante volte il periodo si ripete uguale in un secondo.

In [9]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq  = 4# Frequenza (Hz o cps)

par.sine(freq)

L'orecchio umano nelle sue condizioni ottimali percepisce suoni compresi tra 20 e 20.000 Hz.

Nella seguente tabella i rapporti tra alcune unità di misura appena esposte.

Nota MIDI Rapporto Frequenza (Hz)
Do 60 $1:1$ 261.6
Do# o Reb 61 $\sqrt[12]{2}$ 277.2
Re 62 $\sqrt[12]{2^2}$ 293.7
Re# o Mib 63 $\sqrt[12]{2^3}$ 311.1
Mi 64 $\sqrt[12]{2^4}$ 329.6
Fa 65 $\sqrt[12]{2^5}$ 349.2
Fa# o Solb 66 $\sqrt[12]{2^6}$ 370.0
Sol 67 $\sqrt[12]{2^7}$ 390.0
Sol# o Lab 68 $\sqrt[12]{2^8}$ 415.3
La 69 $\sqrt[12]{2^9}$ 440.0
La# o Sib 70 $\sqrt[12]{2^{10}}$ 466.2
Si 71 $\sqrt[12]{2^{11}}$ 493.9
Do 72 $2:1$ 523.3

Implicazioni musicali Indice

Nella tradizione musicale occidentale i rapporti fra le altezze sono stati il primo parametro che è stato organizzato secondo regole specifiche:

  • relazioni orizzontali (Viderunt Omnes - Perotinus - 1200 ca.).
In [10]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/viderunt.mov"></video></center>')
Out[10]:
  • sovrapposizioni di voci orizzontali (Nuper rosarum Flores - G.Dufay - 1436)
In [11]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/ruper.mov"></video></center>')
Out[11]:
  • relazioni verticali (Toccata quarta del sesto tono - C.Merulo - 1600 ca.)
In [12]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/merulo.mov"></video></center>')
Out[12]:
  • costruzioni formali (Canone VI - J.S.Bach (1741))
In [13]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/bach_can.mov"></video></center>')
Out[13]:

Dinamica o ampiezza Indice

Questo parametro in termini musicali è dato dal rapporto tra i suoni più deboli (pianissimissimo) e quelli più forti che caratterizzano la dinamica di un brano.

Misurazioni e rappresentazioni Indice

La dinamica di un suono in fisica si definisce con il termine ampiezza in quanto descrive l’ampiezza delle variazioni dell’onda sonora rispetto allo stato di quiete e fornisce una misura dell’energia da essa trasportata.

Se prendiamo in considerazione l'aspetto fisico acustico e non la percezione umana questo parametro è indipendente dalla frequenza e per convenzione rappresentato da valori compresi tra -1.0 e +1.0.

In [14]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq  = 8         # Frequenza (Hz o cps)
amp   = 0.2        # Ampiezza (tra 0.0 e 1.0)

par.vsine(freq, amp) 
par.sine(freq, amp)

Il termine ampiezza è troppo generico e per evitare confusione aggiungiamo un aggettivo per distinguere tre differenti modalità di misurazione:

  • Ampiezza istantanea - La misura del valore di energia in un preciso istante nel tempo. Valori compresi tra -1.0 e 1.0. Nella rappresentazione dei segnali su un piano cartesiano, il valore misurato sull'asse delle ordinate (y) in un punto preciso sull'asse delle ascisse (x). Nell'audio digitale è il valore di un singolo campione.
  • Ampiezza di picco - il valore assoluto di energia più alto tra le ampiezze istantanee comprese in un tempo finito. Valori compresi tra 0.0 e 1.0. Se il Valore più alto è negativo togliamo il meno.
  • Root Mean Square (RMS) - una particolare media dei valori di energia delle ampiezze istantanee comprese in un tempo finito. Valori compresi tra 0.0 e 1.0.
    • insieme finito di ampiezze istantanee - ( 0.0, 1.5, 1.0, 0.4, 0.6, 0.0, -0.4, -0.2, -1.0, -1.5, 0.0 )
    • elevate al quadrato (square) - ( 0.0, 2.25, 1.0, 0.16, 0.36, 0.0, 0.16, 0.04, 1.0, 2.25, 0.0)
    • media matematica (mean) - 0.65636363636364
    • radice quadrata (root) - 0.81016272215132
In [15]:
import numpy as np
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

n = 12                                # Numero di valori
a = par.amp(n)                        # Valori ampiezza istantanea
print('Ampiezze istantanee: ' + str(a))

a = np.abs(a)                         # Valori assoluti
a = np.amax(a)                        # Restituisce il valore più alto
print('Ampiezza di picco: ' + str(a))

a = par.amp(n)                        # Valori ampiezza istantanea
a = a**2                              # Eleva al quadrato
a = np.mean(a)                        # Calcola la media aritmetica
a = np.sqrt(a)                        # Calcola la radice quadrata
a = np.round_(a, 2)                   # Approssima a due decimali
print('Root Mean Square: ' + str(a))

par.img(n) 

Ampiezze istantanee: [ 0.    0.86  0.65  0.34  0.59  0.34 -0.61 -0.85 -0.21 -0.04 -0.34  0.03]
Ampiezza di picco: 0.86
Root Mean Square: 0.5

La principale differenza tra ampiezza di picco e RMS sta nel fatto che la prima è un valore univoco indipendente dall'andamento del segnale mentre la seconda essendo una media è strettamente legata all'andamento dell'inviluppo del segnale.

In [16]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.sf('media/pizz.wav')
par.sf('media/tenuto.wav')

Ampiezza di picco: 0.88
Root Mean Square: 0.12

Ampiezza di picco: 0.91
Root Mean Square: 0.25

In musica è importante misurare non solo le ampiezze ma anche i rapporti che intercorrono tra suoni con intensità differenti.

Questo parametro è anche comunemente chiamato volume o fattore di amplificazione e possiamo rappresentarlo in due diversi modi:

  1. Simboli musicali - I valori sono quasi sempre relativi al contesto musicale, ovvero un "forte" in una sonata per violino barocca non ha la stessa intensità di un "forte" dato agli ottoni in un poema sinfonico di R.Strauss. A differenza delle altezze dove esiste una corrispondenza precisa tra la rappresentazione simbolica in notazione musicale e la misurazione fisica, le dinamiche musicali sono caratterizzate da una rilevante soggettività che va ben oltre alla semplice misura fisica delle ampiezze dei suoni.
In [17]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Dinamiche.png" width="36%"></center>')
Out[17]:
  1. Valori numerici relativi a diverse unità di misura che si riferiscono tutte all'ampiezza di picco:
  • Lineare - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più lontana dalla percezione umana riguardo i cambiamenti di intensità dei suoni. Un suono con ampiezza di 0.5 sarà sempre la metà del suono "più forte possibile" e avrà sempre la stessa intensità indipendentemente dal contesto musicale.
  • Key Velocity (MIDI) - Unità di misura assoluta espressa in valori interi compresi tra 0.0 e 1.0. La meno precisa a causa del limitato numero di livelli dovuto alla disponibilità di soli 7 bit del protocollo MIDI. Un suono con una key velociy di 127 sarà sempre "il più forte possibile" e avrà sempre la stessa intensità indipendentemente dal contesto musicale.

  • Quartica - Unità di misura assoluta espressa in valori decimali compresi tra 0.0 e 1.0. La più vicina alla percezione umana riguardo i cambiamenti di intensità dei suoni. Per calcolare i valori corretti dobbiamo elevare l'ampiezza lineare alla quarta potenza. Essendo compresi tra 0.0 e 1.0 l'ambito (range) rimane lo stesso.

    $$a^4$$

  • Decibels (dB) - Unità di misura relativa espressa in valori decimali compresi tra 0.0 e -inf (o +inf a seconda del tipo di misurazione). Misura la differenza di intensità tra l'ampiezza di un suono rispetto a un'ampiezza di riferimento. Un suono con ampiezza di -6.02 dB sarà sempre forte la metà rispetto a un suono la cui ampiezza è stata presa come riferimento per la misurazione. Per calcolare i valori corretti dobbiamo utilizzare la seguente formula dove $a$ è il valore dell'ampiezza lineare del suono che vogliamo misurare mntre $a0$ è l'ampiezza del suono di riferimento (1.0).

    $$20*\log_{10}(\frac{a}{a0})$$

In [18]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.curve()

Alcuni rapporti tra queste unità di misura.

Segno Vel lin quart dB
pppp 12 0.1 0.0001 -20
ppp 24 0.2 0.0016 -14
pp 44 0.3 0.0081 -10
p 54 0.4 0.0256 -8
mp 64 0.5 0.0625 -6
mf 74 0.6 0.1296 -4
f 84 0.7 0.2401 -3
ff 94 0.8 0.4096 -2
fff 114 0.9 0.6561 -1
ffff 127 1.0 1.0000 0

E formule di conversione

In [19]:
import numpy as np

ampvel = 0.5 * 127
velamp = 64  / 127 

ampqrt = 0.5**4 
qrtamp = pow(0.0625, 1/4)  # radice ennesima di x = x**(1/radice ennesima)
ampdb  = 20 * np.log10(0.5)
dbamp  = 10**(-6/20)

print(ampvel)
print(velamp)
print(ampqrt)
print(qrtamp)
print(ampdb)
print(dbamp)

63.5
0.5039370078740157
0.0625
0.5
-6.020599913279624
0.5011872336272722
  • Phon - o livello di sensazione sonora. Abbiamo affermato che frequenza e ampiezza in quanto parametri fisici del suono sono indipendenti. Nel momento in cui il suono giunge all'orecchio le cose si complicano, infatti il sistema uditivo umano non è formato soltanto dall'orecchio: il modo in cui le informazioni trasmesse dal nervo acustico vengono elaborate dal cervello è, in una certa misura, addirittura più importante delle informazioni stesse. Le informazioni acustiche sono filtrate, selezionate, modificate dal cervello e la percezione dell'intensità dei suoni cambia in relazione alla frequenza legando di fatto i due parametri. Il diagramma di Fletcher e Munson rappresenta la sensibilità dell'orecchio alle diverse frequenze e per diverse pressioni sonore.
  • sull'asse verticale sono presenti le pressioni sonore in dB

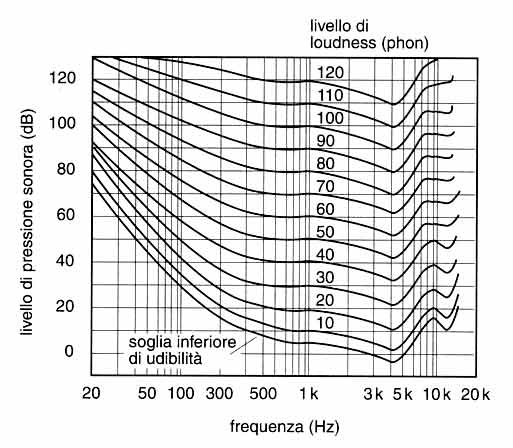
  • sull'asse orizzontale le frequenze in scala logaritmica.

    Le curve, chiamate curve di uguale livello sonoro o isofoniche, dicono quale pressione sonora è necessaria, alle diverse frequenze, per dare la medesima impressione di intensità. L'unità di misura è il phon che rappresenta dunque l'udibilità soggettiva dell'orecchio umano, che in determinati casi, non coincide con la differenza oggettiva che due suoni hanno tra loro.

In [20]:
from IPython.display import HTML 
HTML('<center><img src="esempi/isofoniche.png" width="40%"></center>')
Out[20]:

Implicazioni musicali Indice

Nella tradizione musicale occidentale i rapporti fra le dinamiche sono stati il terzo parametro (dopo tempo e ritmo) che è stato organizzato secondo specifiche modalità a fini espressivi:

  • piani sonori contrapposti per sottolineare fraseggio e struttura formale (Piano quartet KV 478 - W.A.Mozart 1785).
In [21]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/mozart.mov"></video></center>')
Out[21]:
  • crescendo e diminuendo per sottolineare fraseggio ed espressività (Piano Concert - R.Schumann - 1845)
In [22]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/schumann.mov"></video></center>')
Out[22]:
  • piani dinamici sfalsati per sottolineare polifonie strumentali (Prelude n° 1 - C.Debussy - 1909)
In [23]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/debussy.mov"></video></center>')
Out[23]:

Strumenti o timbro Indice

Il timbro è quella particolare qualità del suono che permette di distinguere due suoni con uguale ampiezza e altezza e consente all'ascoltatore di identificare la fonte sonora, rendendola distinguibile da ogni altra.

Misurazioni e rappresentazioni Indice

Il timbro dei suoni naturali è influenzato da moltissimi parametri variabili come ad esempio le caratteristiche fisiche dei materiali della sorgente sonora e dal modo in cui è messo in vibrazione.

Tutti questi parametri concorrono a formare una rappresentazione fisica del timbro di quel suono ovvero la sua forma d'onda, che descrive come varia nel tempo la pressione atmosferica (o il voltaggio di un segnale) nel produrre quel determinato suono.

Nelle celle sottostanti sono illustrate tre diverse forme d'onda:

  • suono puro - è formato da una sola onda sinusoidale con propria frequenza, ampiezza e fase. Non esiste in natura e può solo essere sintetizzato
In [24]:
import os
import sys
import IPython.display as ipd
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.puro()
ipd.Audio('media/puro.mp3')

/Users/andreavigani/anaconda3/lib/python3.11/site-packages/matplotlib/cbook/__init__.py:1340: ComplexWarning: Casting complex values to real discards the imaginary part
  return np.asarray(x, float)
Out[24]:
Your browser does not support the audio element.
  • suono complesso periodico - è caratterizzato dalla presenza di più sinusoidi (suoni parziali) sovrapposte, ognuna con una propria frequenza, una propria ampiezza e una propria fase che hanno un qualche tipo di relazione tra loro.
In [25]:
par.periodico()
ipd.Audio('media/periodico.mp3')
Out[25]:
Your browser does not support the audio element.
  • suono complesso aperiodico (rumore) - come il precedente ma i parametri non sono in relazione tra loro.
In [26]:
par.noise()
ipd.Audio('media/noise.mp3')
Out[26]:
Your browser does not support the audio element.

Gli elementi principali che contribuiscono alla caratterizzazione delle forme d'onda sono due:

  • nel dominio della frequenza le componenti spettrali
  • nel dominio del tempo l'inviluppo spettrale

Componenti spettrali o spettri sonori Indice

I suoni presenti in natura non producono mai suoni puri (onde sinusoidali perfette) ma sono caratterizzati da forme d'onda differenti tra loro e dunque da suoni complessi.

Un suono complesso è il risultato della sovrapposizione (somma) di più suoni puri ognuno con frequenza, ampiezza e fase differenti secondo il teorema enunciato dal fisico francese J.Fourier nei primi anni dell'800:

Qualunque segnale periodico può essere scomposto nella somma di un eventuale termine costante e di segni sinusoidali, dei quali il primo, avente lo stesso periodo e quindi la stessa frequenza del segnale considerato, si chiama prima armonica o fondamentale, e gli altri, aventi periodi sottomultipli e quindi frequenze multiple, si chiamano armoniche superiori

In [27]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.fourier()

Per chiarire ulteriormente possiamo pensare uno spettro sonoro come un accordo musicale le cui singole note sono eseguite da suoni sinusoidali (un singolo suono puro per ogni nota) che l'orecchio umano non percepisce come un accordo formato da più note ma come un singolo suono con un determinato timbro.

In [28]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Fourier.png" width="14%"></center>')
Out[28]:

Ogni suono puro che concorre a formare uno spettro complesso può essere chiamato suono armonico o parziale.

La differenza terminologica tra queste due definizioni è sottile e implica la conoscenza del tipo di spettro a cui si riferisce.

Fondamentalmente gli spettri sonori possono essere suddivisi in due grandi famiglie la cui differenziazione è data dai rapporti frequenziali intercorrenti tra le componenti pure che li formano.

Spettri armonici. Le frequenze dei parziali seguono rapporti formati da numeri interi:

  • $1:1$ - Fondamentale
  • $1:2$ - Primo armonico
  • $1:5$ - Quarto armonico
  • $1:8$ - Settimo armonico
  • ...
  • 1:n - Ennesimo armonico

I parziali possono essere chiamati anche armonici dove il suono (usualmente) più grave che corrisponde al rapporto 1:1 è chiamato fondamentale ed è quello che generalmente caratterizza l'altezza percepita di quel suono complesso, mentre i parziali successivi sono chiamati primo armonico, secondo armonico, e via dicendo fino idealmente a infinito.

La forma d'onda di questi suoni complessi può essere solamente periodica.

In questo caso, stabilita la frequenza fondamentale in Hertz per ricavare le frequenze degli armonici basterà moltiplicarne il valore per i numeri interi.

In [29]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Serie_armonica.png" width="63%"></center>')
Out[29]:
In [30]:
from IPython.display import Audio
Audio('media/armonico.mp3')
Out[30]:
Your browser does not support the audio element.

Spettri inarmonici. Le frequenze dei parziali non seguono alcun rapporto particolare, o meglio non sono in rapporto con un suono fondamentale che è assente.

  • $4.0:2.5$ - Primo parziale
  • $1.2:8.7$ - Secondo parziale
  • $1.4:2.9$ - Terzo parziale
  • $9.3:5.2$ - Quarto parziale
  • ...
  • $n:n$ - Ennesimo parziale

La forma d'onda di questi suoni può essere sia periodica che aperiodica.

In [31]:
from IPython.display import Audio
Audio('media/inarmonico.mp3')
Out[31]:
Your browser does not support the audio element.

Possiamo affermare che tutti i suoni possibili sono formati da spettri compresi tra:

  • suono puro (la singola sinusoide - periodico) e
  • suono più complesso (il rumore bianco - aperiodico)

le cui caratteristiche oscillano tra suoni inarmonici, suoni quasi armonici e suoni armonici.

In [32]:
import os
import librosa
import IPython.display as ipd
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

sr     = 22050                                # Frequenza di campionamento
path   = os.path.abspath('media/tenuto.wav')  # Path file
offset = 1                                    # Offset in secondi
w_size = 1024                                 # Window size (in samples)

y, sr = librosa.load(path, sr=sr,offset=offset, duration=(1/sr)*w_size) # Assegna le ampiezze istantanee di y

par.plotFFT(y,sr,150)
ipd.Audio('media/tenuto.wav')
Out[32]:
Your browser does not support the audio element.

Inviluppo d'ampiezza Indice

Le tipologie di spettri sonori che abbiamo appena descritto si riferiscono a fotografie di un suono.

Il suono però comincia dal silenzio, segue una parabola ben delineata e scandita in diverse fasi temporali e infine torna al silenzio.

Possiamo schematizzare il susseguirsi di queste fasi nel modo seguente:

  • attacco che corrisponde a come il suono viene generato dal silenzio.
  • fase di sostegno durante la quale generalmente il contenuto spettrale si stabilizza.
  • una fase di decadimento che corrispnde a come il suono torna al silenzio.

Queste tre fasi costituiscono quello che viene definito l'inviluppo d'ampiezza di un suono.

Nella figura sottostante sono illustrati gli inviluppi di ampiezza caratteristici di alcuni strumenti musicali.

In [33]:
from IPython.display import HTML 
HTML('<center><img src="media/envs.png" width="55%"></center>')
Out[33]:

Inviluppo spettrale Indice

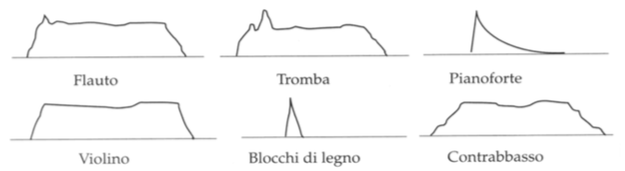
Durante queste fasi il contenuto spettrale del suono emesso non è costante ma varia nel tempo e dunque il timbro di un suono è determinato dall'evoluzione del contenuto spettrale nel tempo.

Ogni singolo parziale segue un proprio inviluppo d'ampiezza, che sovrapposto agli inviluppi degli altri parziali forma l'inviluppo spettrale di un suono.

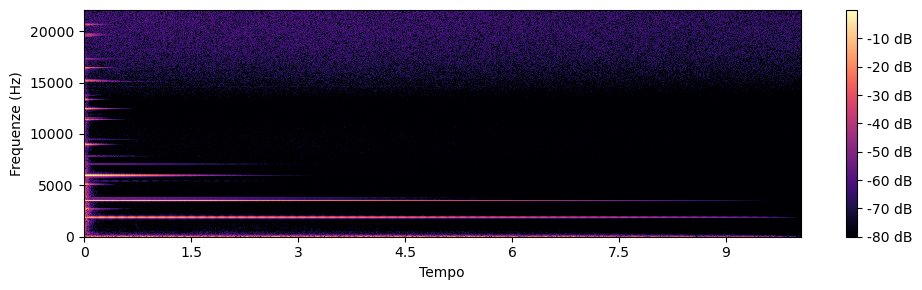
Ad esempio lo spettro del suono di un pianoforte è molto più vicino al rumore bianco al suo attacco (nei primi millisecondi) quando il martelletto colpisce le corde, si stabilizza in uno spettro armonico ricco dato dalle caratteristiche fisiche del corpo dello strumento nella fase di sostegno per poi rarefarsi vero pochi suoni puri di risonanza quasi-armonici nella fase di rilascio.

In [34]:
from IPython.display import HTML 
HTML('<center><img src="media/spettro.png" width="100%"></center>')
Out[34]:
In [35]:
import IPython.display as ipd
ipd.Audio('media/crotalo.wav')
Out[35]:
Your browser does not support the audio element.

Implicazioni musicali Indice

Le relazioni che intercorrono tra sorgente sonora, caratteristiche fisiche dell'onda sonora generata (altezza, intensità e timbro) e la percezione multisensoriale di entrambe sono molto complesse e abbracciano diversi ambiti di studio (psicoacustica, antropologia culturale, neuroscienze, etc.).

Osserviamo un percussionista con un tamburo e una bacchetta.

Nel momento in cui la bacchetta colpisce la pelle dello strumento viene prodotto un suono.

Il nostro cervello dopo aver osservato (percezione visiva) una o più volte il gesto che genera quel determinato suono e aver ascoltato (percezione auditiva ) il suono prodotto da quel determinato gesto crea una connessione tra i due sensi, includendo nella nostra memoria esperenziale queste nuove informazioni.

Con il passare degli anni ed il moltiplicarsi delle esperienze visivo/auditive, nel nostro cervello si crea un immenso database di suoni correlati a oggetti e a gesti che ci permette di immaginare quel determinato tamburo ogni qualvolta ne sentiamo il suono corrispondente, anche attraverso una registrazione, in assenza di uno stimolo visivo.

E' presto detto che ciò vale anche nel caso inverso, ovvero nel momento in cui osserviamo quel tamburo possiamo richiamare alla memoria e "pensare" il suono (o i suoni) che può produrre, così come hanno fatto (quasi) tutti i compositori che non avevano a disposizione campionatori o registratori nell'atto di comporre un brano per uno o più strumenti, e ancor più nell'orchestrare amalgame di timbri più o meno omogenei.

In [36]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/schubert.mov"></video></center>')
Out[36]:

Nel corso della stratificazione culturale propria della tradizione musicale occidentale il timbro è stato il quarto parametro del suono sviluppato organicamente e il processo appena descritto (assieme ad altre importanti concause) ha favorito l'astrazione del pensiero musicale.

Un suono rappresenta se stesso anche simbolicamente e non l'oggetto che lo ha prodotto, svincolandolo dall'esistrere solo ad un livello esperenziale/percettivo.

Tre esempi del percorso timbrico nella storia della musica occidentale.

  • la musica per tastiera di J.S.Bach. Secondo la consuetudine del tempo, l'autore adotta l'indicazione generica "fur Klavier" (per tastiera) nello specificare in partitura la destinazione strumentale di alcune composizioni come le Sei Suites Inglesi BWV 807 (1720 ca.) relegando in questo modo il parametro timbrico e la correlazione suono-strumento ad un ruolo secondario se non del tutto ininfluente rispetto all'informazione musicale trasmessa che è data unicamente dall'organizzazione nel tempo di altezze e intensità.
In [37]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/bach_suite.mov"></video></center>')
Out[37]:
  • la musica del '900 dove il parametro timbrico attraverso lo sviluppo delle tecniche strumentali e l'orchestrazione diviene parte integrante della sintassi e dell'informazione musicale come nel Quartetto Op. 38 di A.Webern - 1938.
In [38]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/webern.mov"></video></center>')
Out[38]:
  • la musica acusmatica che è un tipo di musica elettroacustica dove suoni registrati, elaborati o generati da computer sono fissati su un supporto e diffusi in concerto da uno o più altoparlanti.

Le caratteristiche estetiche e le sintassi che stanno alla base di questa forma d'arte risiedono proprio nel principio di non riconoscibilità della sorgente sonora.

"...rumore acusmatico si dice di un suono che si ascolta senza scoprirne le cause. Ebbene, questa è la definizione stessa dell'oggetto sonoro, questo elemento di base della musica concreta, musica la più generale che sia, di cui la testa sarebbe vicino al cielo e i cui piedi toccherebbero il regno dei morti..." (J. Peignot)

Partendo da questa idea i suoni impiegati in queste composizioni vengono organizzati nel tempo attraverso sistemi di regole i cui elementi sintattici sono i parametri fisico/morfologici del suono stesso dove il timbro è il parametro principale.

Non esiste un oggetto/strumento che produce suono ma un oggetto sonoro che è suono ri-prodotto (e non prodotto) da sistemi (orchestre) di altoparlanti chiamati acusmonium.

In [39]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/acusmatica.mov"></video></center>')
Out[39]:
In [40]:
from IPython.display import HTML 
HTML('<center><img src="media/acusmonium.png" width="60%"></center>')
Out[40]:

A partire dal secondo '900 nella musica d'arte inoltre si è sviluppata una corrente musicale che persegue la creazione di un musica acusmatica strumentale dove il timbro storicizzato di strumenti acustici appartenenti alla tradizione musicale occidentale viene snaturato in oggetto sonoro destoricizzato sia attraverso l'impiego di mezzi elettroacustici (elaborazione del suono in tempo reale e la sua diffusione) sia atterverso l'impiego di tecniche strumentali aumentate (multifonici, col legno, soffi, etc.) come nel brano di L.Nono "...a Pierre, dell'azzurro silenzio, inquietum" - 1985

In [41]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/nono.mov"></video></center>')
Out[41]:

Fase e moto armonico Indice

Misurazioni e rappresentazioni Indice

Nel paragrafo precedente abbiamo osservato come, secondo il teorema di Fourier tutti i suoni possono essere scomposti come sommatoria di sinusoidi ognuna con una propria frequenza, una propria ampiezza e una propria fase.

La funzione sinusoidale può rappresentare una legge oraria chiamata moto armonico semplice che è un moto periodico lungo un asse rettilineo detto origine (O).

$x(t) = a * sin(\omega t + \varphi)$

Dal punto di vista cinematico può essere visto come:

  • Il punto blu si muove per moto circolare uniforme sulla circonferenza, lungo il diametro.
    • La sua velocità è costante.
  • il punto rosso è la sua proiezione sull'asse x e continua a oscillare lungo i due estremi del diametro con l'origine al centro dell'oscillazione.
    • La sua velocità non è costante, è massima al centro e nulla agli estremi.
    • L'accelerazione è massima agli estremi e nulla al centro.
  • Il punto verde è la rappresentazione nel tempo.
In [42]:
from IPython.display import HTML 
HTML('<center><video width="95%" controls loop autoplay> <source src="media/sine.mp4"></video></center>')
Out[42]:
  • La massima distanza dall'origine è l'Ampiezza del moto e va da -1 a +1.
  • la durata di un'oscillazione completa rispetto l'origine è il Periodo e corrisponde a $2\pi$ (360°).
  • L'origine dell'oscillazione è la sua Fase.
In [43]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

freq = 5    # Cambia i parametri...
amp  = 1
fase = 0.5 

par.sinepar(freq,amp,fase)

Implicazioni musicali Indice

I concetti fisici di periodo e fase sono stati impiegati anche come regole procedurali in diverse sintassi della tradizione musicale occidentale.

Pensiamo al retrogrado, all'inversione o alle tecniche contrappuntistiche dell'epoca barocca oppure nel secondo '900 ai compositori minimalisti come S.Reich.

In [44]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/reich.mov"></video></center>')
Out[44]:

Disposizione o spazializzazione Indice

Strettamente correlato al parametro timbro e alle relazioni tra sorgente sonora e percezione dell'informazione musicale c'è il parametro spazio che è l'ultimo in ordine di tempo indagato a fini espressivi nella tradizione musicale occidentale anche se nel passato ci sono stati periodi in cui era già entrato a far parte della sintassi musicale dell'epoca come nei brani per cori spezzati nella Venezia di fine '500.

In [45]:
from IPython.display import HTML 
HTML('<center><img src="media/cori.png" width="60%"></center>')
Out[45]:

Musica su supporto - diffusione tramite altoparlanti che possono essere posizionati a piacere nell'ambiente d'ascolto realizzando spazi acustici inediti.

In [46]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/stocki.mov"></video></center>')
Out[46]:

Live electronics - relazioni percettive complesse tra la sorgente sonora acustica (strumenti) e sorgenti sonore virtuali (altoparlanti).

In [47]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/boulez_dialogue.mov"></video></center>')
Out[47]:
In [48]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/laptop.mov"></video></center>')
Out[48]:

Tempo e pulsazioni Indice

La misurazione del tempo è stata la prima scienza esatta dell’antichità.

Le uniche certezze provenivano dai fenomeni astronomici.

I suoni (e di conseguenza la musica) esistono solo nel tempo, in un tempo non reversibile se non nella memoria.

Per questo motivo dobbiamo definire alcuni parametri atti a misurare il tempo, o meglio misurare una sequenza di eventi o azioni che si svolgono nel tempo per poterli organizzare (comporre) in ritmo e tradurli in linguaggi simbolici interpretabili da esecutori umani o da software.

Misurazioni e rappresentazioni Indice

Possiamo specificare qualsiasi tipo di evento sonoro nel tempo scegliendo almeno due tra i seguenti parametri:

  • Onsets - tempi assoluti incrementali a partire da un tempo 0 iniziale.
In [49]:
from IPython.display import HTML 
HTML('<center><img src="esempi/Onsets.png" width="40%"></center>')
Out[49]:
  • Tempi delta - la misurazione del tempo che intercorre tra due eventi consecutivi.
In [50]:
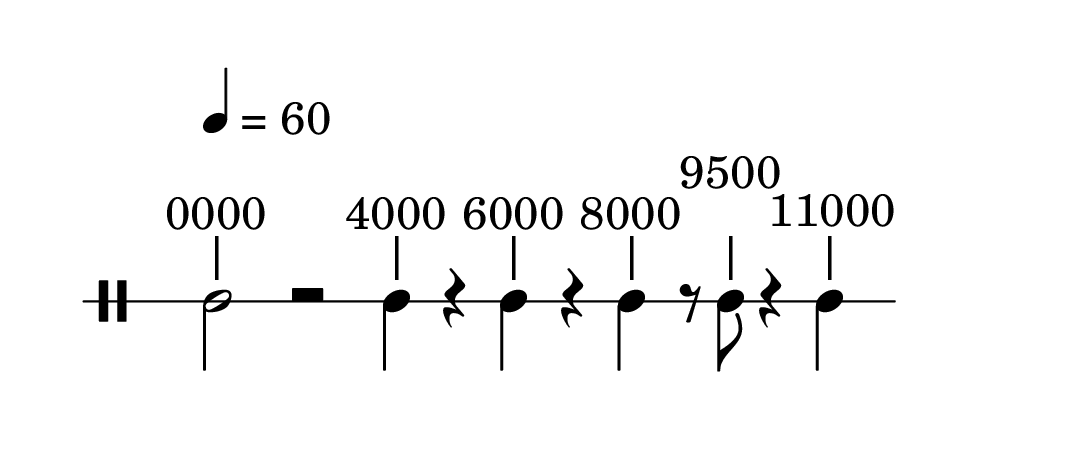
from IPython.display import HTML 
HTML('<center><img src="esempi/DeltaT.png" width="40%"></center>')
Out[50]:
  • Durate - la misurazione della durata di uno o più eventi.
In [51]:
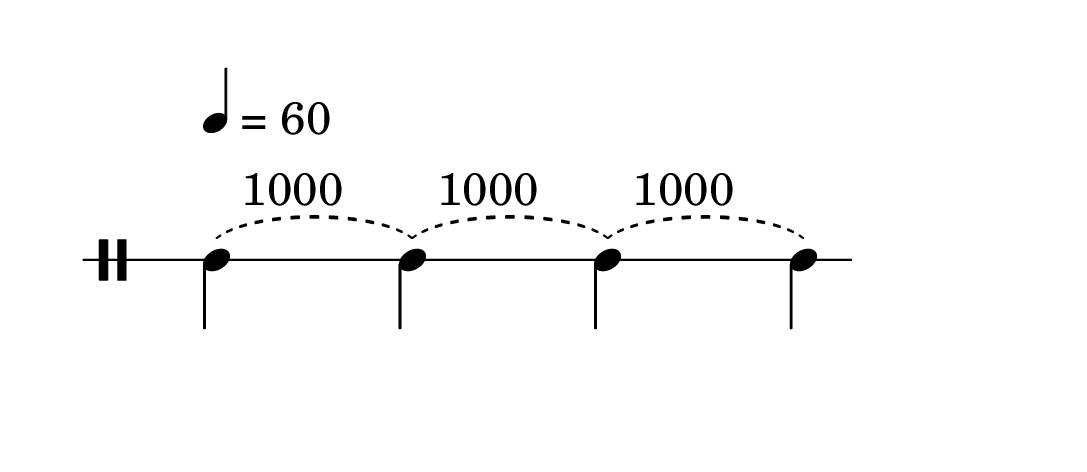
from IPython.display import HTML 
HTML('<center><img src="esempi/Durate.png" width="60%"></center>')
Out[51]:

A seconda delle situazioni e degli ambienti software possiamo impiegare oppure la coppia tempi delta e durate come nell'immagine precedente oppure la coppia onset e durate come nelle daw oppure nella rappresentazione MIDI sotto forma di piano roll.

In entrmbe i casi se:

  • tempo delta = durata - legato
  • tempo delta < durata - pause tra gli eventi
  • tempo delta > durata - sovrapposizione polifonica
In [52]:
import os
import sys
sys.path.insert(0, os.path.abspath('moduli')) 
import parametri as par                                                              
%matplotlib inline

par.proll("esempi/Bach_1.mid")

Unità di misura Indice

Possiamo specificare ognuno di questi parametri attraverso due unità di misura differenti.

Tempo assoluto

Proprio dei linguaggi informatici, non è in alcun modo relativo alle regole di alcun sistema musicale di riferimento.

Unità di misura:

  • Secondi
  • Millisecondi
In [ ]:
onsets = (0.0,  0.25, 0.5, 1)   # secondi
durate = (0.25, 0.25, 0.5, 2)
delta  = (  0.25, 0.25, 0.5)

onsets = (0.0,  250, 500, 1000) # millisecondi
durate = (250, 250, 500, 2000)
delta  = (  250, 250, 500)

Tempo relativo

Tutti i valori sono definiti attraverso suddivisioni di una pulsazione regolare e può essere relativo alle regole di un sistema musicale di riferimento

Unità di misura (beat):

  • Battiti per minuto (bpm) o tempo metronomico - l’unità di misura musicale per antonomasia.
  • Battiti per secondo (bps) o cps o Hz - unità di misura più usata in fisica e in informatica.

Possiamo rappresentare i valori in quattro modi diversi.

  • Notazione simbolica - sistema di simboli (grafici, alfabetici o altro) e regole codificate.
  • Notazione frazionale - numero di suddivisioni del beat (1/4).
  • Fattore di moltiplicazione dell'unità - valore numerico corrispondente al risultato della notazione frazionale (0.5).
  • Notazione proporzionale - ratio (proporzione) tra suddivisioni del beat (3:2).
In [53]:
from IPython.display import HTML       
print(' ')
print("Simboli numerici          16    16     8    2    4")       
print("Simboli alfabetici         s     s     e    h    q")  
print("Notazione frazionale     1/4   1/4   1/2   2/1  1/1 (beat = quarto = 1)") 
print("Fattori moltiplicazione  0.25  0.25  0.5    2    1  (beat = quarto = 1)")
print("Notazione proporzionale  1:4   1:4   2:4   8:4  4:4 (quantità : n_suddivisioni_beat)")  
print("Simboli musicali")   
HTML('<center><img src="esempi/Ritmo.png" width="36%"></center>')

 
Simboli numerici          16    16     8    2    4
Simboli alfabetici         s     s     e    h    q
Notazione frazionale     1/4   1/4   1/2   2/1  1/1 (beat = quarto = 1)
Fattori moltiplicazione  0.25  0.25  0.5    2    1  (beat = quarto = 1)
Notazione proporzionale  1:4   1:4   2:4   8:4  4:4 (quantità : n_suddivisioni_beat)
Simboli musicali
Out[53]:

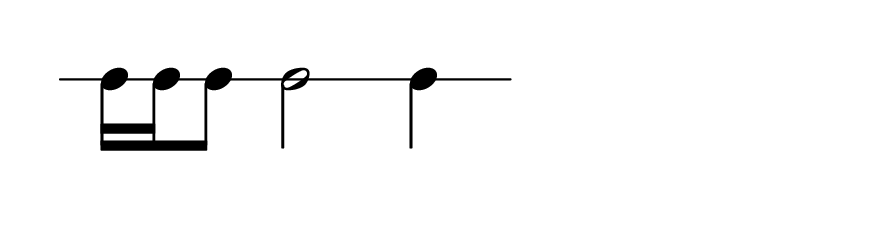
Possiamo convertire facilmente le unità di misura temporali.

In [54]:
bpm = 78

print(bpm/60)    # bpm --> bps
print(60000/bpm) # bpm --> ms
print(60/bpm)    # bpm -->  s

bps = 1.3
print(bps*60)    # bps --> bpm

sec = 0.5
print(1/sec)     # sec --> Hz (bps)

Hz = 4
print(1/Hz)      # Hz --> sec

1.3
769.2307692307693
0.7692307692307693
78.0
2.0
0.25

Implicazioni musicali Indice

Nel corso dei secoli l’uomo è passato dal ritmo naturale che ha a che fare con la ciclicità degli eventi che accadono in natura al ritmo musicale, basato invece su di una pulsazione regolare finita o infinita:

In [55]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/bach_cello.mov"></video></center>')
Out[55]:

Dai greci a oggi il senso del tempo musicale si è modificato enormemente.

Dal battito regolare del Tactus (la sillaba breve) alla de-costruzione dello stesso in pulsazioni irregolari e poliritmie strutturali perseguite dai compositori europei e statunitensi nel secolo scorso, fino al ritorno di un beat ossessivo nella musica dei compositori minimalisti e nei diversi generi di musica Pop/Rock.

La seguente Figura illustra uno schema che comprende tutte le possibili tipologie di pulsazioni esistenti siano esse suddivisioni di un beat o meno.

In [56]:
from IPython.display import HTML 
HTML('<center><img src="media/schema_puls.png" width="80%"></center>')
Out[56]:

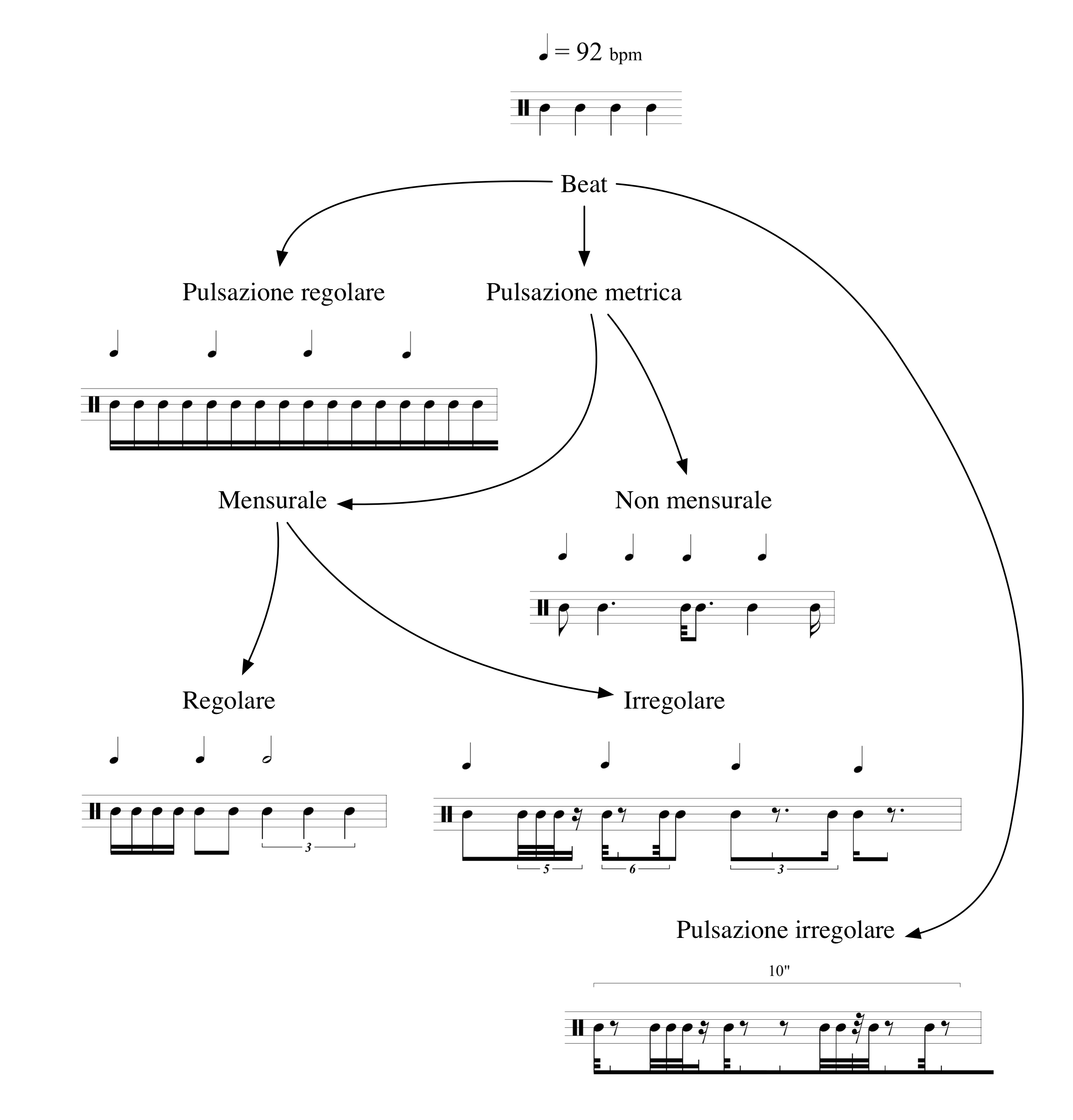
Regolare

Questo tipo si pulsazione può:

  • Coincidere con il beat o esserne una suddivisione costante.
  • Assumere valenza formale come in Piano phase di S.Reich
  • Caratterizzare un brano come nei Perpettum mobile.
  • Costruire griglie di poliritmi polifonici.
  • Diventare elemento timbrico in processi di sintesi ed elaborazione del suono (battimenti, ribattuti, tremolo, sintesi granulare, etc.).
In [57]:
from IPython.display import HTML 
import numpy as np

a = [0.25 for i in range(4)]
print(a)
HTML('<center><img src="media/puls_reg.png" width="40%"></center>')

[0.25, 0.25, 0.25, 0.25]
Out[57]:
In [58]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/piano_phase.mov"></video></center>')
Out[58]:

Metrica mensurale regolare

Figure ritmiche caratterizzanti e riconoscibili all’ascolto (pattern) che si ripetono uguali o variate nel corso dell’intera sequenza.

L’insieme di un gruppo di suddivisioni deve essere contenuto all’interno di un singolo beat o di suoi multipli.

E’ la pulsazione che ha caratterizzato la storia della musica occidentale dagli esordi fino ai giorni nostri.

Su di essa si basa tutta la teoria musicale occidentale, intesa sia come insieme di metodi per analizzare, classificare e comporre la musica e i suoi elementi, sia come relazioni tra la semiografia (notazione musicale) e la sua esecuzione.

Il suo percorso storico parte idealmente dalla ritmica greca, passa per il canto gregoriano e viene sviluppata con l’avvento della polifonia e del mensuralismo.

Codificata in teoremi di diversa natura, diventa un sistema unitario di organizzazione del tempo musicale che si sviluppa ulteriormente fino alle complesse vicende linguistiche del secondo ‘900.

In [59]:
from IPython.display import HTML 
import numpy as np

a = 1/np.array([4 for i in range(4)])
b = 1/np.array([2 for i in range(2)])
c = 2/np.array([3 for i in range(3)])

print(a)
print(b)
print(np.round_(c,6))
HTML('<center><img src="media/puls_mmr.png" width="30%"></center>')

[0.25 0.25 0.25 0.25]
[0.5 0.5]
[0.666667 0.666667 0.666667]
Out[59]:
In [60]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/mozart_piano.mov"></video></center>')
Out[60]:

Metrica mensurale irregolare

In questa tipologia è perseguito il risultato musicale opposto rispetto a quella precedente:

una suddivisione irregolare e continuamente cangiante del beat che annulla la percezione di figure ritmiche riconoscibili all’ascolto e del beat stesso, relegandolo a semplice griglia temporale non espressa in millisecondi o secondi ma in bpm raggruppati o meno in misure musicali.

In [61]:
from IPython.display import HTML 
import numpy as np

a = 1/np.array([2,10,10,10,5])
b = 1/np.array([12,3,12,2])
c = 1/np.array([3,2,6])
d = 1/np.array([4,1.33])

print(np.round_(a,2))
print(np.round_(b,2))
print(np.round_(c,2))
print(np.round_(d,2))
HTML('<center><img src="media/puls_mmi.png" width="50%"></center>')

[0.5 0.1 0.1 0.1 0.2]
[0.08 0.33 0.08 0.5 ]
[0.33 0.5  0.17]
[0.25 0.75]
Out[61]:
In [62]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/boulez_piano.mov"></video></center>')
Out[62]:

Metrica non mensurale

Anche questo tipo di pulsazione corrisponde a una suddivisione del beat.

L’insieme di un gruppo di suddivisioni non è però necessariamente raggruppato in un beat o suoi multipli.

E’ simile alla precedente tipologia ma non ”imbrigliata” all’interno di misure.

Si presta a operazioni musicali di ritmica polimetrica e a creare brevi sequenze ritmiche percettivamente riconoscibili, ripetute più volte in loop (patterns irregolari).

Nel rappresentalra in notazione musicale spesso è utilizzata una scrittura proporzionale in campo aperto con o senza indicazione di misure.

In [63]:
from IPython.display import HTML 
import numpy as np

a = 1/np.array([6,4,7,3,3,7,6])

print(np.round_(a,2))
HTML('<center><img src="media/puls_mnm.png" width="35%"></center>')

[0.17 0.25 0.14 0.33 0.33 0.14 0.17]
Out[63]:
In [64]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/messiaen.mov"></video></center>')
Out[64]:

Irregolare

Questo tipo di pulsazione corrisponde a una suddivisione irregolare assoluta di un tempo misurato in secondi o millisecondi.

Non c’è alcun tipo di relazione e rappresenta in un certo senso l’assenza se non la negazione della pulsazione.

La notazione può essere tradizionale in campo aperto.

Il beat non deve essere percepito, anche in presenza di cellule ritmiche.

In [65]:
from IPython.display import HTML 
import numpy as np

a = np.array([0.12,0.23,1.23,0.56,2.58,2.56])

print(np.round_(a,2))
HTML('<center><img src="media/puls_irr.png" width="40%"></center>')

[0.12 0.23 1.23 0.56 2.58 2.56]
Out[65]:
In [66]:
from IPython.display import HTML 
HTML('<center><video width="60%" controls> <source src="media/stock.mov"></video></center>')
Out[66]: