from IPython.display import HTML
HTML('<center><img src="media/Pwm.png" width="55%"></center>')
Questo Notebook vuole fornire le conoscenze teoriche e relizzative che riguardano le principali tecniche di sintesi ed elaborazione del suono in tempo differito.
Le applicazioni di queste tecniche riguardano il sound design per la composizione di brani acusmatici o di musica mista, per i più diversi ambiti della musica applicata come commenti sonori a immagini e filmati, musica per videogames, installazioni audio e audio/video, etc.
SuperCollider
// Tutte allocazioni di memoria
// ----------------------------------------------------------------
// Array (Client side)
// 0 1 2 Indici
a = [12, 23, 34]; // Items
a.plot; // Visualizza il contenuto (tasto 'm' cambia vista)
a = [\ciao, \miao, 34.5, SinOsc.ar]; // Qualsiasi tipo di data
// ----------------------------------------------------------------
// Buffer (Server side)
(
s.boot;
s.scope;
{s.plotTree}.defer(1)
)
// E' un 32-bit floating point Array multicanale.
// E' associata una rata di campionamento (che può essere diversa
// da quella del Server dove è riservato).
b = Buffer.alloc(s, 100, 1); // server, samples, n_chan
// Ad ogni Buffer viene assegnato un indice partendo da 0
b.free; // Distrugge il Buffer
Buffer.freeAll; // Distrugge tutti i buffers sul Server
// Tre possibili utilizzi:
// ---------------> 1 Caricare soundfiles
b = Buffer.read(s, "voce.wav".resolveRelative);
b.play; // Monitor uditivo
b.plot; // Monitor visivo
b.free;
// ---------------> 2 Riservare uno spazio di memoria vuoto da
// riempire con segnali provenienti da una
// sorgente (microfoni o oscillatori)
b = Buffer.alloc(s, s.sampleRate * 2, 1); // 2 secondi...
SynthDef.new(\rec, {RecordBuf.ar(SoundIn.ar,c,loop:0,doneAction:2)}).play
b.play; // Monitor uditivo
b.plot; // Monitor visivo
b.free;
// ---------------> 3 Wavetable - Riservare uno spazio di memoria
// vuoto di dimensioni ridotte (512, 1024, 2048
// 4096, 8192 samples) in cui disegnare un singolo
// ciclo di forma d'onda o altro tipo di data
// come ad esempio i risultati di un'analisi FFT,
// una tranfert functions, etc...
b = Buffer.alloc(s, 512, 1); // 512 campioni...
b.sine1([1,0.5,0.7,0.3],true,false);
SynthDef.new(\rec, {Out.ar(0,OscN.ar(b)*0.2)}).play;
b.plot; // Monitor visivo
b.free;
//=================================================================
// Il size dei Buffer è in campioni e non da alcuna indicazione
// riguardo alla durata del Buffer se non viene messo in relazione
// con la rata di campionamento...
// ----------------------------------------------------------------
// Rappresentazione (Array)
(
a = (0..30);
b = Signal.sineFill(30,[0.4,0.6,0.2]);
[a,b].plot(discrete:true);
)
// ----------------------------------------------------------------
// Audio (Buffer)
(
s.boot;
s.scope;
{s.plotTree}.defer(1)
)
b.free;
b = Buffer.read(s, "voce.wav".resolveRelative);
(
SynthDef.new(\play, {var pha, sig;
pha = Phasor.ar(0,MouseY.kr(0,10),0,BufFrames.kr(b));
pha.linlin(0,BufFrames.kr(b),0,1).scope;
sig = BufRd.ar(1,b,pha);
Out.ar(0,sig*0.2)}
).add;
)
Synth.new(\play);
b.free;
b = Buffer.alloc(s, 512, 1); // 512 campioni...
b.sine1([1,0.5,0.7,0.3],true,false);
//=================================================================
// Tipologie di oscillatori
(
s.boot;
s.scope;
{s.plotTree}.defer(1)
)
// ----------------------------------------------------------------
// PlayBuf (Sample playback oscillator)
Buffer.freeAll;
b = Buffer.read(s, "voce.wav".resolveRelative);
b.plot;
b.play;
(
SynthDef(\ply1, {var sig;
sig = PlayBuf.ar(1,b,doneAction:2);
Out.ar(0,sig)
}).add;
)
Synth(\ply1);
// ----------------------------------------------------------------
// BufRD (Buffer reading oscillator)
(
SynthDef(\ply2, {var sig;
sig = BufRd.ar(1,b,LFNoise2.ar(1) * BufFrames.kr(b));
Out.ar(0,sig)
}).add;
)
a = Synth(\ply2);
a.free;
// ----------------------------------------------------------------
// Osc (Interpolating wavetable oscillator)
b.free;
b = Buffer.alloc(s, 512, 1);
b.sine1(1.0/[1,2,3,4,5,6], true, true, true);
b.plot;
(
SynthDef(\ply3, {var sig;
sig = Osc.ar(b,MouseY.kr(200,800) * 0.4);
Out.ar(0,sig!2)
}).add;
)
a = Synth(\ply3);
a.free;
//=================================================================
// Possiamo definire il timbro di un suono disegnandone la forma
// d'onda calcolando ogni singolo valore di ampiezza istantanea
// attraverso una Funzione.
t = {arg a, b; a + b};
t.value(2,4); // argomenti = INPUT risultato = OUTPUT
// ---------------> Funzione Sinusoide
// x[n] = a * sin(w * n + O)
// x = OUTPUT
// [n] = INPUT
// Per ogni n in INPUT calcola un valore corrispondente in OUTPUT
// che corrisponde al valore di ampiezza istantanea:
t = {arg a,w,n; a * sin(w * 1 * n + 0)};
t.value(1, 0.01, 0);
t.value(1, 0.01, 1);
t.value(1, 0.01, 2);
t.value(1, 0.01, 3);
//...
// Automatizziamo il calcolo e collezioniamo i risultati in un Array
(
~punti = 32; // Numero di punti (size della tavola)
~freq = 1; // Numero di cicli per size della tavola
~amp = 1.0; // Ampiezza di picco
~w = 2pi/(~punti/~freq); // Calcolo della velocità angolare (rad/sec)
p = ~punti.collect({arg n; ~amp * sin(~w * n + 2pi)}); // n assume ad ogni valutazione
// l'indice dell'Array
// partendo da 0
p.plot(discrete:true); // Visualizza
)
//=================================================================
// In SuperCollider possiamo generare forme d'onda in due modi:
// • Con la Classe Signal che genera un FloatArray (32 bit float)
// e supporta operazioni matematiche Client side).
// • Invocando alcuni metodi d'istanza dedicati direttamente su di
// un Buffer (Server side).
//=================================================================
// Signal
// Attraverso la classe Signal possiamo disegnare diverse forme
// d'onda utili in svariate tecniche di analisi, sintesi ed
// elaborazione del suono, al momento ne analizziamo solo due:
// ---------------> Genera una sinusoide o uno Spettro armonico:
~punti = 32;
~amp = [1.0]; // Array...
~amp = [0.2,0.5,0.3];
// (Numero di punti, [Ampiezze di picco], [fasi])
p = Signal.sineFill(~punti, ~amp, [2pi]);
p.plot(discrete:true);
// ---------------> I valori y sono calcolati attraverso una Funzione:
p = Signal.newClear(~punti); // Crea un FloatArray di n 0
p.waveFill({arg i; i.postln}, -1, 1); // i valori tra min e max
// ---------------> Funzione della sinusoide...
// sin(x) dove x è compresa tra 0 e 2pi (angolo giro)
(
p.waveFill({arg i;
sin(i)}, // operazioni matematiche (funzioni) su i
0, 2pi); // min, max
)
p.plot(discrete:true);
// ----------------------------------------------------------------
// Da Signal a Buffer
// Per poter essere letti da un Oscillatore dobbiamo caricare i
// valori di generati in un Buffer (Signal genera un'Array che è
// Client side...)
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(1)
)
Buffer.freeAll;
b = Buffer.loadCollection(s, p);
b.plot;
// ----------------------------------------------------------------
// Wavetable format
// Possiamo trasformare un FloatArray (ma non un Array di altro tipo)
// in un formato ottimizzato per la rilettura da parte di Oscillatori
// tabellari che realizzano una Interpolazione lineare come Osc.ar()
// e che si chiama waveteble format.
// In questo formato il numero di campioni deve essere un multiplo di
// due.
p.postln;
w = p.asWavetable; // Trasforma il FloatArray in formato wavetable
w.plot;
// Se trasformato in wavetable format il numero di campioni è RADDOPPIATO:
p.size; // FloatArray
w.size; // Wavetable format (il doppio...)
// Per questo motivo dovremo utilizzare un Buffer size doppio
Buffer.freeAll;
b = Buffer.alloc(s, ~punti * 2);
b.loadCollection(w);
b.plot;
2pi
Buffer.freeAll;
b = Buffer.loadCollection(s, w); // Resize automatico...
// Possiamo salvare il Buffer come sound file:
b.write("/Users/andreavigani/Music/SuperCollider Recordings/suono_1.aiff");
//=================================================================
// Buffer
// (metodi .sine1 .sine2 e .sine3)
(
~punti = 1024;
Buffer.freeAll;
b = Buffer.alloc(s,~punti);
b.sine1([0.3,0.7,1.2], // Ampiezze dei parziali
true, // Normalizza
true, // asWavetable
true); // Cancella prima
{b.plot}.defer(0.1)
)
x = {Osc.ar(b, 200, 0, 0.2)}.play;
x.free;
(
~punti = 1024;
Buffer.freeAll;
b = Buffer.alloc(s,~punti);
b.sine2([1, 2, 3], // Rapporti di frequenza dei parziali
// (solo spettri armonici - numeri interi)
[0.3,0.7,1.2], // Ampiezze dei parziali
true, // Normalizza
true, // asWavetable
true); // Cancella prima
{b.plot}.defer(0.1)
)
x = {Osc.ar(b, 200, 0, 0.2)}.play;
x.free;
(
~punti = 1024;
Buffer.freeAll;
b = Buffer.alloc(s,~punti);
b.sine3([1, 2, 3], // Rapporti di frequenza dei parziali
[0.5,0.3,0.2], // Ampiezze dei parziali
[2pi,pi,0.3pi], // Fasi dei parziali
true, // Normalizza
true, // asWavetable
true); // Cancella prima
{b.plot}.defer(0.1)
)
x = {Osc.ar(b, 200, 0, 0.2)}.play;
x.free;
//=================================================================
// Non interpolating wavetable lookup oscillator
// Si prendono i valori y (ampiezze istantanee) di un fasore (onda
// a dente di sega) per richiamare gli indici di una Wavetable
// all'interno della quale abbiamo memorizzato un eriodo di una
// qualsiasi forma d'onda.
// I valori del fasore sono generalmente compresi tra -1 e +1 nel
// caso di un'onda bipolare oppure tra 0 e +1 (nel caso di un onda
// unipolare).
(
~size = 100; // Size del Buffer
~unipolare = Signal.newClear(~size);
~bipolare = Signal.newClear(~size);
~unipolare.waveFill({arg i; i}, 0, 1);
~bipolare.waveFill({arg i; i}, -1, 1);
[~unipolare,~bipolare].plot(minval:-1,maxval:1,discrete:true);
)
// Per poter impiegare i valori di ampiezza istantanea (y) del
// fasore come indici (x) della wavetable dobbiamo però riscalarli
// in un ambito (range) commpreso tra 0 e il size-1 della wavetable
// da rileggere semplicemente moltiplicando l'onda unipolare per il
// size (nel caso fosse bipolare dobbiamo prima renderla unipolare).
(
~fasore = ~unipolare * ~size; // Fasore tra 0 e size-1
~wave = ~size.collect({arg n; (1 * sin(2pi/p * 1 * n + 0)) + // Primo armonico
(1 * sin(2pi/p * 2 * n + 0)) + // Secondo armonico
(1 * sin(2pi/p * 3 * n + 0)) // Terzo armonico
}); // 1 periodo wavetable
~wave = ~wave.normalize(-1,1); // Tra +/-1
[~fasore++~fasore++~fasore++~fasore,~wave++~wave++~wave++~wave].plot(discrete:true);
)
// Un periodo del fasore coincide con un periodo della wavetable
// e dunque la frequenza del fasore (in Hz) determina anche la
// frequenza dell'oscillatore tabellare.
//=================================================================
// Audio
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(1)
)
//-----------------------------------------------------------------
// Disegnamo in un Buffer una forma d'onda periodica (un ciclo).
(
Buffer.freeAll;
~size = 1024;
b = Buffer.alloc(s,~size);
b.sine1([0.3,0.7,1.2], asWavetable:false); // In formato normale...
{b.plot}.defer(0.1)
)
//-----------------------------------------------------------------
// Creiamo un fasore.
// Ci sono due diverse tecniche per disegnare un fasore:
// ---------------> 1 Oscillatore a dente di sega (riscalato)
// LFSaw.ar()
(
{[
LFSaw.kr(2), // Bipolare
LFSaw.kr(2,-1), // Fuori fase
LFSaw.kr(2,-1)*0.5+0.5, // Unipolare
]}.plot(1)
)
{LFSaw.kr(2,-1)*0.5+0.5*~size}.plot(1) // Riscalato tra 0 e n-1
// In questo caso la frequenza in Hz del fasore sarà la frequenza
// dell'onda riletta.
// ---------------> 2 Contatore a sample rate (wrap around)
// Phasor.ar()
// In questo caso alla velocità della sample rate incrementa di uno
// step (che può essere 1 o altro) e c'è un wrap around tra un
// valore minimo e un valore massimo.
{Phasor.ar(0, 1, 0, 100)}.plot(0.01)
// Se vogliamo stabilire una frequenza in Hz dobbiamo effettuare
// qualche operazione per determinare il fattore di incremento
// size del Buffer * freq(Hz) / sample rate
100 * 440 / 48000; // Incremento = 0.91666666666667
(
{ Phasor.ar(0,
// recupera il size recupera la sample rate attuale
BufFrames.kr(b) * 20 / SampleRate.ir,
0, // Frame inizo lettura
BufFrames.kr(b))}.plot(0.1) // Frame fine lettura
)
//-----------------------------------------------------------------
// Con BufRd.ar()
(
SynthDef(\wave1, {arg buf=b, freq=500, amp=0, dur=1, atk=0.1,t_gate=0,pan=0,done=0,int=1;
var punta,sig,bpf,env,pann;
punta = LFSaw.ar(freq,-1).range(0, BufFrames.kr(buf)); // .range...
sig = BufRd.ar(1, // Numero canali
buf, // Buffer da leggere
punta, // Segnale puntatore
1, // Loop
int); // Interpolazione: 1, 2, 4
bpf = Env.perc(atk*dur, (1.0-atk)*dur);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
// Interpolazione: osservare le differenze nello spettroscopio...
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,1,\done,2,\t_gate,1]); // No interp.
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,2,\done,2,\t_gate,1]); // Interp. lin
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,4,\done,2,\t_gate,1]); // Interp. cub
(
SynthDef(\wave2, {arg buf=b, freq=500, amp=0, dur=1, atk=0.1,t_gate=0,pan=0,done=0,int=1;
var punta,sig,bpf,env,pann;
punta = Phasor.ar(0,
BufFrames.kr(buf) * freq / SampleRate.ir,
0, BufFrames.kr(buf));
sig = BufRd.ar(1, // Numero canali
buf, // Buffer da leggere
punta, // Segnale puntatore
1, // Loop
int); // Interpolazione: 1, 2, 4
bpf = Env.perc(atk*dur, (1.0-atk)*dur);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
// Interpolazione: osservare le differenze nello spettroscopio...
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,1,\done,2,\t_gate,1]); // No interp.
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,2,\done,2,\t_gate,1]); // Interp. lin
Synth(\wave2, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\int,4,\done,2,\t_gate,1]); // Interp. cub
//=================================================================
// BufRD è un oscillatore generico che può essere utilizzato in
// diverse tecniche di rilettura di un Buffer. Per la wavetable
// Synthesis ci sono degli Oscillatori dedicati.
//-----------------------------------------------------------------
// OscN.ar()
// Oscillatore tabellare che non interpola
// Il Buffer deve obbligatoriamente contenere un numero di campioni
// pari a una potenza di 2 e NON ESSERE in WAVETABLE FORMAT.
(
Buffer.freeAll;
~size = 1024;
b = Buffer.alloc(s,~size);
b.sine1([0.3,0.7,1.2], asWavetable:false); // In formato normale...
SynthDef(\oscN, {arg buf=b, freq=500, amp=0, dur=1,t_gate=0,pan=0,done=0;
var sig,bpf,env,pann;
sig = OscN.ar(buf,freq);
bpf = Env.triangle(dur);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
Synth(\oscN, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\dur,0.3,\done,2,\t_gate,1]);
//-----------------------------------------------------------------
// Osc.ar()
// Oscillatore tabellare con interpolazione lineare
// Il Buffer deve obbligatoriamente contenere un numero di campioni
// pari a una potenza di 2 ed ESSERE in WAVETABLE FORMAT.
(
Buffer.freeAll;
~size = 1024;
b = Buffer.alloc(s,~size);
b.sine1([0.3,0.7,1.2], asWavetable:true); // In wavetable format
// La sintassi è identica a OscN
SynthDef(\osc, {arg buf=b, freq=500, amp=0, dur=1,t_gate=0,pan=0,done=0;
var sig,bpf,env;
sig = Osc.ar(buf,freq);
bpf = Env.triangle(dur);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0,sig)}
).add;
)
Synth(\osc, [\buf,b,\freq,rrand(70,82).midicps,\amp,1,\dur,0.3,\done,2,\t_gate,1]);
// SinOsc è come quest'ultimo Synth che legge un Buffer interno di 8192 campioni
//=================================================================
// Sintesi additiva a spettro fisso con frequenze in rapporto
// armonico.
// Possiamo generare una forma d'onda che produca uno spettro
// armonico con la possibilità di controllare per ogni parziale:
// • Rapporto di frequenze
// • Ampiezze
// • Fasi
// Possiamo impiegare uno a scelta tra i metodi illustrati nel
// paragrafo dedicato alle funzioni d'onda
//=================================================================
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
//-----------------------------------------------------------------
// Buffer
(
~punti = 2048;
Buffer.freeAll;
b = Buffer.alloc(s,~punti);
b.sine3([1, 2, 3], // Rapporti di frequenza dei parziali
[0.5,0.3,0.2], // Ampiezze dei parziali
[2pi,2pi,2pi], // Fasi dei parziali
true, // Normalizza
true, // asWavetable
);
{b.plot(bounds:600@400, minval: -1, maxval:1)}.defer(0.1)
)
//-----------------------------------------------------------------
// Strumento
(
SynthDef(\wave, {arg buf=b, freq=500, amp=0, dur=1, fade=0.1,t_gate=0,pan=0,done=0;
var sig,bpf,env,pann;
sig = Osc.ar(buf,freq);
bpf = Env.linen(fade, dur-(fade*2),fade,curve:\cub);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
//-----------------------------------------------------------------
// Sound design 1 - Organo
Synth(\wave, [\buf,b,\amp,0.4,\freq,rrand(60,72).midicps,\done,2,\t_gate,1]);
//-----------------------------------------------------------------
// Sound design 2 - Run
(
r = Routine.new({
inf.do({
~amps = 10.collect({rand(1.0)}).normalizeSum;
~phas = 10.collect({rand(2pi)});
p = Signal.sineFill(~punti/2, ~amps, ~phas);
p = p.asWavetable;
b.loadCollection(p);
Synth(\wave, [\buf,b,
\freq,500,
\amp,rand(1.0),
\dur,rrand(0.05,0.08),
\fade,0.01,
\pan, [-1,1].choose,
\done,2,
\t_gate,1]);
0.1.wait;
})
}).play
)
r.reset.play; // Suona
r.stop; // Stoppa
//-----------------------------------------------------------------
// Sound design 3 - Tappeto sonoro
(
~amps = 10.collect({rand(1.0)}).normalizeSum;
~phas = 10.collect({rand(2pi)});
p = Signal.sineFill(~punti/2, ~amps, ~phas);
b = Buffer.loadCollection(s, p.asWavetable);
v = Routine.new({
inf.do({
Synth(\wave, [\buf,b,
\freq,rrand(50,100).midicps, // Atonale
// \freq, [68,72,75,80].midicps.choose, // Triade
\amp,rand(1.0),
\dur,rrand(4,8),
\fade,rrand(0.2,8),
\pan, rand2(1.0),
\done,2,
\t_gate,1]);
rrand(0.1,2).wait;
})
}).play
)
v.reset.play; // Suona
v.stop; // Stoppa
//=================================================================
// Sintesi additiva a spettro fisso con frequenze in rapporto
// armonico.
// Possiamo generare una forma d'onda che produca uno spettro
// armonico con la possibilità di controllare per ogni parziale:
// • Rapporto di frequenze
// • Ampiezze
// • Fasi
// Possiamo impiegare uno a scelta tra i metodi illustrati nel
// paragrafo dedicato alle funzioni d'onda
//=================================================================
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
//-----------------------------------------------------------------
// Buffer
(
~punti = 2048;
Buffer.freeAll;
b = Buffer.alloc(s,~punti);
b.sine3([1, 2, 3], // Rapporti di frequenza dei parziali
[0.5,0.3,0.2], // Ampiezze dei parziali
[2pi,2pi,2pi], // Fasi dei parziali
true, // Normalizza
true, // asWavetable
);
{b.plot(bounds:600@400, minval: -1, maxval:1)}.defer(0.1)
)
//-----------------------------------------------------------------
// Strumento
(
SynthDef(\wave, {arg buf=b, freq=500, amp=0, dur=1, fade=0.1,t_gate=0,pan=0,done=0;
var sig,bpf,env,pann;
sig = Osc.ar(buf,freq);
bpf = Env.linen(fade, dur-(fade*2),fade,curve:\cub);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
//-----------------------------------------------------------------
// Sound design 1 - Organo
Synth(\wave, [\buf,b,\amp,0.4,\freq,rrand(60,72).midicps,\done,2,\t_gate,1]);
//-----------------------------------------------------------------
// Sound design 2 - Run
(
r = Routine.new({
inf.do({
~amps = 10.collect({rand(1.0)}).normalizeSum;
~phas = 10.collect({rand(2pi)});
p = Signal.sineFill(~punti/2, ~amps, ~phas);
p = p.asWavetable;
b.loadCollection(p);
Synth(\wave, [\buf,b,
\freq,500,
\amp,rand(1.0),
\dur,rrand(0.05,0.08),
\fade,0.01,
\pan, [-1,1].choose,
\done,2,
\t_gate,1]);
0.1.wait;
})
}).play
)
r.reset.play; // Suona
r.stop; // Stoppa
//-----------------------------------------------------------------
// Sound design 3 - Tappeto sonoro
(
~amps = 10.collect({rand(1.0)}).normalizeSum;
~phas = 10.collect({rand(2pi)});
p = Signal.sineFill(~punti/2, ~amps, ~phas);
b = Buffer.loadCollection(s, p.asWavetable);
v = Routine.new({
inf.do({
Synth(\wave, [\buf,b,
\freq,rrand(50,100).midicps, // Atonale
// \freq, [68,72,75,80].midicps.choose, // Triade
\amp,rand(1.0),
\dur,rrand(4,8),
\fade,rrand(0.2,8),
\pan, rand2(1.0),
\done,2,
\t_gate,1]);
rrand(0.1,2).wait;
})
}).play
)
v.reset.play; // Suona
v.stop; // Stoppa
A questo link possiamo scaricare una cartelle contenente numerose wavetables sotto forma di sound files.
/=================================================================
// Sintesi Vettoriale
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
//-----------------------------------------------------------------
// Array di Buffer
(
Buffer.freeAll;
b = Buffer.allocConsecutive(4, // Numero di Buffer
s, // Server
1024); // Size di ogni singolo Buffer (multiplo di 2)
)
(
b[0].sine1([1,0.3,0.5,0.7],true,true); // asWavetable !!!
b[1].sine1([0.2,0.4,1.3,0.6],true,true);
b[2].sine1([1,0.2,0.5,0.6,1.3,0.5],true,true);
b[3].sine1([1.3,0.3,0.5,0.7,0.8,0.9,0.2,0.3],true,true);
)
b.at(0);
b[3].plot;
b.do(_.free); // libera l'Array di Buffer
//-----------------------------------------------------------------
// Sintesi vettoriale
(
SynthDef(\vec_1, {arg buf=0,bufn=4,freq=400,amp=0,pan=0,gate=0,done=2;
var pos,sig,env;
pos = MouseX.kr(buf,bufn.asFloat).poll(10);
sig = VOsc.ar(pos, freq);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0, sig)
}).add;
)
a = Synth(\vec_1, [\buf,b[0],\bufn,b.size-1,\freq,400,\amp,1,\pan,0,\gate,1]);
a.set(\gate,0);
//-----------------------------------------------------------------
// Mapping parametri
// Un solo valore controlla il timbro...due (quattro) possibilità
// di controllo.
// -------> 1) Timbro mappato argomenti
// Per maggiore compatibilità meglio stabilire un range tra -1 e + 1
(
SynthDef(\vec_2, {arg buf=0,bufn=4,pos= -1,freq=400,amp=0,pan=0,gate=0,done=2;
var sig, env;
sig = VOsc.ar(pos.linlin(-1,1,buf,bufn).lag(0.02), freq);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0, sig)
}).add;
)
a = Synth(\vec_2, [\buf,b[0],\bufn,b.size-1,\freq,400,\amp,1,\pan,0,\gate,1]);
a.set(\pos,rand2(1.0).postln);
a.set(\gate,0);
// -------> 2) Timbro mappato su segnale di controllo esterno
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(-1,1).poll(10);
Out.kr(busOut,sig)
}).add;
{m = Synth(\mouse, [\busOut, ~mouseY])}.defer(1); // Synth per ksig
a = Synth(\vec_2, [\buf,b[0],\bufn,b.size-1,
\freq,400,\amp,1,\pan,0,\gate,1],
s, \addToTail); // Deve essere dopo il Synth del Mouse
)
a.set(\pos,~mouseY.asMap); // Mappa il parametro sul control bus...
a.set(\pos,rand2(1.0).postln); // Scollega il bus...
a.set(\gate,0); m.free;
// -------> 3) Timbro mappato sull'inviluppo d'ampiezza
(
SynthDef(\vec_3, {arg buf=0,bufn=4,freq=400,dur=1,amp=0,pan=0,t_gate=0,done=2;
var sig,bpf,env;
bpf = Env.sine(dur);
env = EnvGen.ar(bpf,t_gate,doneAction:done);
sig = VOsc.ar(env.linlin(0,1,buf,bufn-1), freq);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0, sig)
}).add;
)
(
Synth(\vec_3, [\buf,b,\bufn,4,
\freq,rrand(70, 96).midicps,
\dur,rrand(1,8),
\amp,rand(1.0),
\pan,rand2(1.0),
\t_gate,1]);
)
// -------> 4) Timbro mappato su segnale di controllo interno
(
SynthDef(\vec_4, {arg buf=0,bufn=4,freq=400,kfreq=0.5,dur=1,amp=0,pan=0,gate=0,done=2;
var sig,ksig,env;
env = Linen.kr(gate,doneAction:done);
// ksig = MouseY.kr(buf,bufn.asFloat);
ksig = LFNoise1.kr(kfreq).range(buf,bufn-1); // Ksig riscalato
sig = VOsc.ar(ksig, freq);
sig = Pan2.ar(sig * amp * env, pan);
Out.ar(0, sig)
}).add;
)
(
a = Synth(\vec_4, [\buf,b,\bufn,4,
\freq,rrand(70, 96).midicps,
\dur,rrand(0.1,2),
\amp,rand(1.0),
\pan,rand2(1.0),
\gate,1]);
)
a.set(\kfreq,2);
a.set(\kfreq,0.7);
a.set(\gate,0);
//-----------------------------------------------------------------
// Chorusing
(
SynthDef(\vec_3, {arg buf=0,bufn=4,freq=#[440,445,435],amp=0,pan=0,gate=0,done=2;
var pos,sig,env,pann;
pos = LFNoise1.kr(0.2).range(0.0,bufn-1);
sig = VOsc3.ar(pos, freq[0],freq[1],freq[2]);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig*amp.lag(2)*env);
Out.ar(0, pann)
}).add;
)
(
a = Synth(\vec_3, [\buf,b[0],
\bufn,b.size-1,
\freq, 3.collect({rrand(200,1000)}).postln,
\amp,0.3,
\pan,0,
\gate,1]);
)
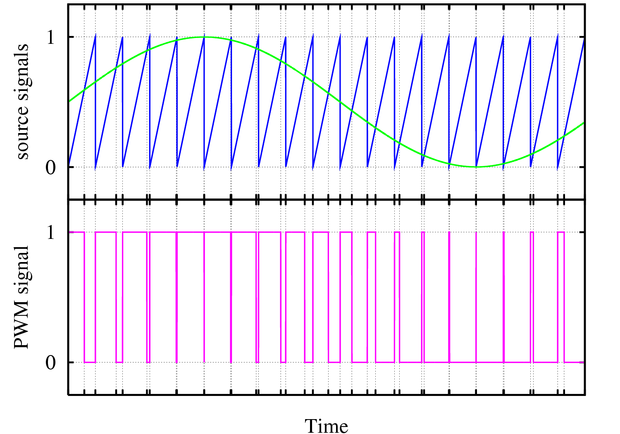
La PWM è utilizzata per molti scopi, per quanto ci riguarda i principali dono due:
codificare segnali analogici continui in segnali digitali confrontandone i valori di ampiezza istantanea con quelli di un'onda a dente di sega o triangolare avente una frequenza almeno dieci volte maggiore dell'ampiezza di banda del segnale da codificare. In questo modo il duty cycle aumenta in modo proporzionale all'ampiezza del segnale in ingresso.
tecnica di sintesi del suono per ottenere spettri complessi che possono variare dinamicamente nel tempo.
from IPython.display import HTML
HTML('<center><img src="media/Pwm.png" width="55%"></center>')

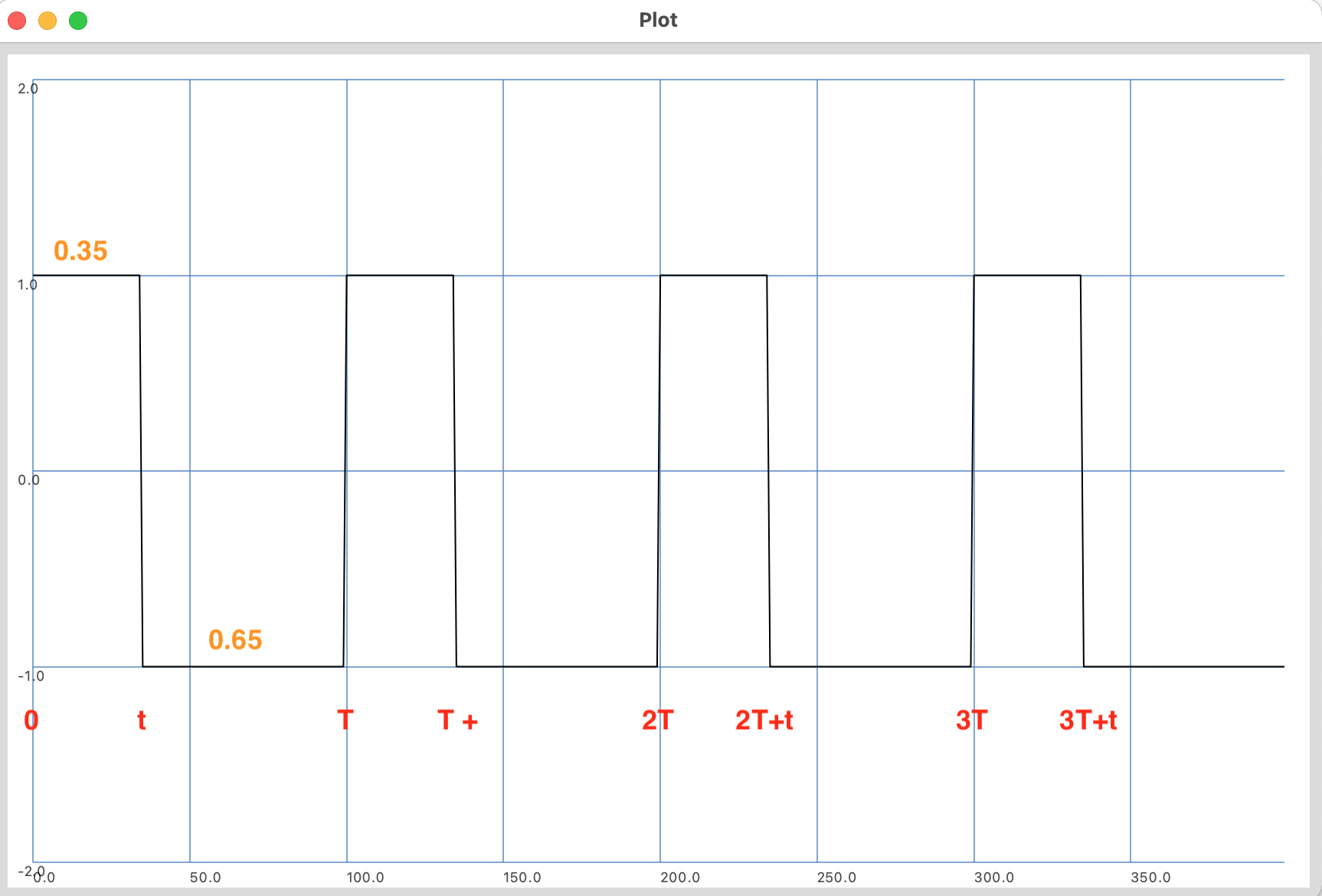
Duty cycle ([d] - ciclo di lavoro)
E' la frazione di tempo (t) che un'entità passa in stato attivo rispetto ad un ciclo totale (T) e possiamo esprimerla in questo modo:
$d = t/T$
Il valore ottenuto sarà sempre compreso tra 0.0 e 1.0 che sono i suoi limiti rappresentanti due SEGNALI CONTINUI:
from IPython.display import HTML
HTML('<center><img src="media/Duty_cy.png" width="55%"></center>')
//-----------------------------------------------------------------
// Pulse.ar()
// Consideriamo un ONDA QUADRA o TRENO DI IMPULSI che ha un duty
// cycle di 0.5 (1/2). Il suo spettro è caratterizzato dalla presenza
// dei soli armonici dispari ovvero 1:2 la cui ampiezza decade secondo
// la formula 1/numero_di_armonico.
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
(
SynthDef(\pulse_1, {arg freq=300, duty=0.5,amp=0,gate=0,pan=0,done=2;
var sig,env;
sig = Pulse.ar(freq, duty);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * amp * env,pan);
Out.ar(0,sig)}
).add;
)
a = Synth(\pulse_1, [\amp,0.5,\duty,1/2,\gate,1]);
// armonici presenti:
// 1 3 5 7 9 11 13 15 17 19 21 ...
a.set(\duty,1/2);
// Se modifichiamo il duty cycle in 1/3 (0.333) un armonico su tre
// sarà assente e avremo quindi i seguenti armonici:
a.set(\duty,1/3);
// 1 2 4 5 7 8 10 11 13 14 16 17 19 20 ...
// Se modifichiamo il duty cycle in 1/4 (0.25) un armonico su quattro
// sarà assente e avremo quindi i seguenti armonici:
a.set(\duty,1/4);
// 1 2 3 5 6 7 9 10 11 13 14 15 17 18 19 21 ...
// Continuando s diminuire il duty cycle possiamo notare come
// l'ampiezza globale (overall amplitude) si abbassa (i tempi di
// silenzo in ogni ciclo sono maggiori) mentre la distribuzione
// dell'energia lungo lo spettro tende ad appiattirsi.
a.set(\duty,1/5);
a.set(\duty,1/10);
a.set(\duty,1/15);
a.set(\duty,1/20);
a.set(\duty,1/25);
a.set(\duty,1/30);
a.set(\duty,1/40);
a.set(\duty,1/50);
a.set(\duty,1/100);
a.set(\duty,1/1000);
a.set(\duty,1/5000);
a.set(\duty,1/44100);
a.set(\gate,0);
// Il duty cycle minimo reale di un sistema audio digitale è di
// 1/sample_rate il cui spettro idealmente è caratterizzato dalla
// presenza di tutti i suoni armonici ognuno dei quali con la stessa
// ampiezza.
{Impulse.ar}.plot
//-----------------------------------------------------------------
// Impulse.ar()
// In questo caso possiamo utilizzare la UGen Impulse che normalizza
// l'ampiezza generale a 1.
(
SynthDef(\pulse_2, {arg freq=300,amp=0,gate=0,pan=0,done=2;
var sig,env;
sig = Impulse.ar(freq);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0,sig)}
).add;
)
a = Synth(\pulse_2, [\amp,0.5,\gate,1]);
a.set(\amp,1);
a.set(\freq,rrand(72,90).midicps);
a.set(\gate,0);
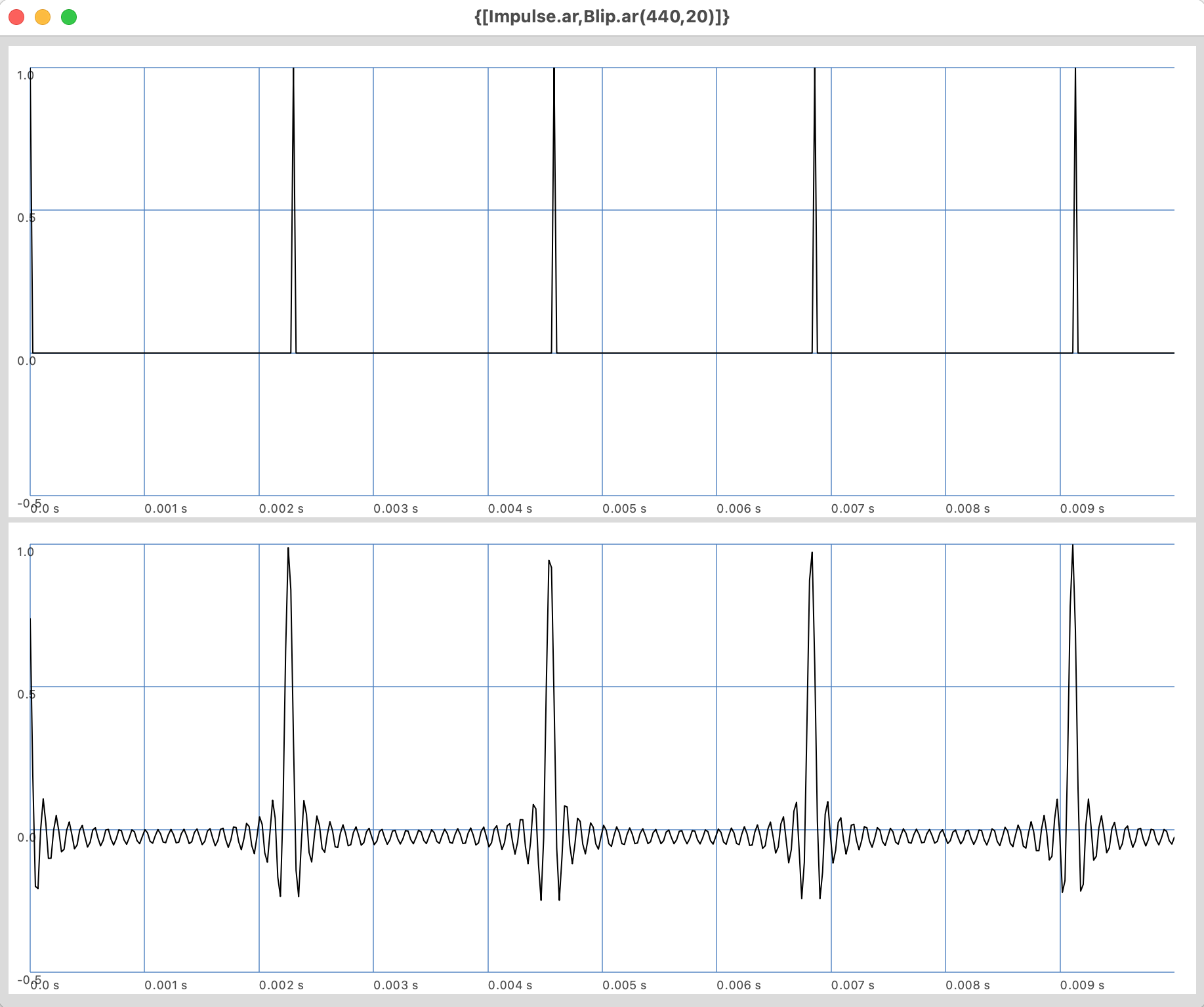
//-----------------------------------------------------------------
// Blip.ar()
// Il segnale generato da Impulse.ar() non è limitato in frequenza
// e può dare origine a fenomeni di ALIASING o FOLDOVER. In
// SuperCollider esiste però un'altra UGen che riproduce un
// oscillatore storico dei linguaggi MusicN (buzz) e che è stato
// implementato in diversi sintetizzatori commerciali degli anni
// '90 come Synth-O-Matic.
{[Impulse.ar,Blip.ar(440,20)]}.plot;
(
SynthDef(\pulse_3, {arg freq=300,nharm=20,amp=0,gate=0,pan=0,done=2;
var sig,env;
sig = Blip.ar(freq,nharm);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*amp*env,pan);
Out.ar(0,sig)}
).add;
)
a = Synth(\pulse_3, [\amp,0.5,\gate,1]);
a.set(\nharm,10);
a.set(\nharm,3);
a.set(\nharm,[3,13,100].choose);
a.set(\gate,0);
// Fino a questo punto abbiamo preso in considerazione solo
// duty cycle compresi tra 1/2 o 0.5 (onda quadra) e 1/sr ma non
// quelli tra 0.5 e 1. Fortunatamente i comportamenti dello spettro
// in questo caso sono speculari: un segnale con duty cycle di 0.4 ha
// lo stesso spettro di uno con duty cycle di 0.6, uno con 0.3 e
// uno di 0.7 e così via...
a = Synth(\pulse_1, [\amp,0.5,\duty,0.5,\gate,1]);
a.set(\duty,0.4);
a.set(\duty,0.6);
a.set(\duty,0.3);
a.set(\duty,0.7);
a.set(\gate,0);
//-----------------------------------------------------------------
// VarSaw.ar()
(
SynthDef(\pulse_4, {arg freq=300, duty=0.5,amp=0,gate=0,pan=0,done=2;
var sig,env;
sig = VarSaw.ar(freq,0,duty);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * amp * env,pan);
Out.ar(0,sig)}
).add;
)
a = Synth(\pulse_4, [\amp,0.5,\duty,1/2,\gate,1]);
a.set(\duty,1/3);
a.set(\duty,1/4);
a.set(\duty,1/5);
a.set(\gate,0);
from IPython.display import HTML
HTML('<center><img src="media/Impulsi.png" width="55%"></center>')
//-----------------------------------------------------------------
// Mapping parametri
// Un solo valore controlla il timbro...due (quattro) possibilità
// di controllo.
// -------> 1) Timbro mappato argomenti
// Per maggiore compatibilità meglio stabilire un range tra -1 e + 1
(
SynthDef(\pulse_5, {arg freq=300, dur=0.1,duty=0.5,amp=0,t_gate=0,pan=0,done=2;
var sig,env;
sig = VarSaw.ar(freq, 0, duty);
env = EnvGen.ar(
Env.perc(0.1*dur,0.9*dur),
t_gate,doneAction:done);
sig = Pan2.ar(sig * amp * env,pan);
Out.ar(0,sig)}
).add;
)
(
r = Routine.new({
inf.do({
Synth(\pulse_5, [\freq,300,\dur,0.2,\amp,0.5,\duty,rand(0.5),\t_gate,1]);
0.1.wait;
})
}).play
)
// -------> 2) Timbro mappato su segnale di controllo esterno
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(0.5,0); // Tra 0.5 e 0
Out.kr(busOut,sig)
}).add;
{m = Synth(\mouse, [\busOut, ~mouseY])}.defer(1); // Synth per ksig
)
(
r = Routine.new({
inf.do({
Synth(\pulse_5, [\freq,300,\dur,0.2,\amp,0.5,
\duty,~mouseY.asMap, // Mappato sul Bus di controllo
\t_gate,1],
s,\addToTail); // Dopo Synth Mouse
0.1.wait;
})
}).play
)
// -------> 3) Timbro mappato sull'inviluppo d'ampiezza
(
SynthDef(\pulse_6, {arg freq=300, dur=0.1,amp=0,t_gate=0,pan=0,done=2;
var sig,env,duty;
env = EnvGen.ar(
Env.perc(0.1*dur,0.9*dur),
t_gate,doneAction:done);
duty = env.linlin(0,1,0.5,0); // Riscalato...
sig = VarSaw.ar(freq, 0, duty);
sig = Pan2.ar(sig * amp * env,pan);
Out.ar(0,sig)}
).add;
)
Synth(\pulse_6, [\freq,rrand(60,72).midicps,\dur,2,\amp,0.5,\t_gate,1]);
a = Synth(\pulse_6, [\amp,0.5,\duty,1/2,\gate,1]);
// -------> 4) Timbro mappato su segnale di controllo interno
(
SynthDef(\pulse_7, {arg freq=300,amp=0,gate=0,pan=0,done=2;
var duty,sig,env,pann;
duty = MouseX.kr(0.5,0);
sig = VarSaw.ar(freq,0,duty);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig * amp * env,pan);
Out.ar(0,pann)}
).add;
)
a = Synth(\pulse_7, [\amp,0.5,\duty,1/2,\gate,1]);
(
SynthDef(\pulse_8, {arg freq=300,gate=0,pan=0,done=2;
var duty,amp,sig,env,pann;
amp = LFNoise1.kr(1).unipolar;
duty = LFNoise1.kr(1).range(0,0.5);
sig = VarSaw.ar(freq,0,duty);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig * amp * env,pan);
Out.ar(0,pann)}
).add;
)
(
a = Synth(\pulse_8, [\freq,300,\amp,0.3,\duty,1/2,\pan, -1,\gate,1]);
b = Synth(\pulse_8, [\freq,301,\amp,0.3,\duty,1/4,\pan, 1,\gate,1]);
)
a.set(\gate,0); b.set(\gate,0);
Ricordiamo la Wavetable Lookup Synthesis.
from IPython.display import HTML
HTML('<center><img src="media/Lookup.png" width="55%"></center>')
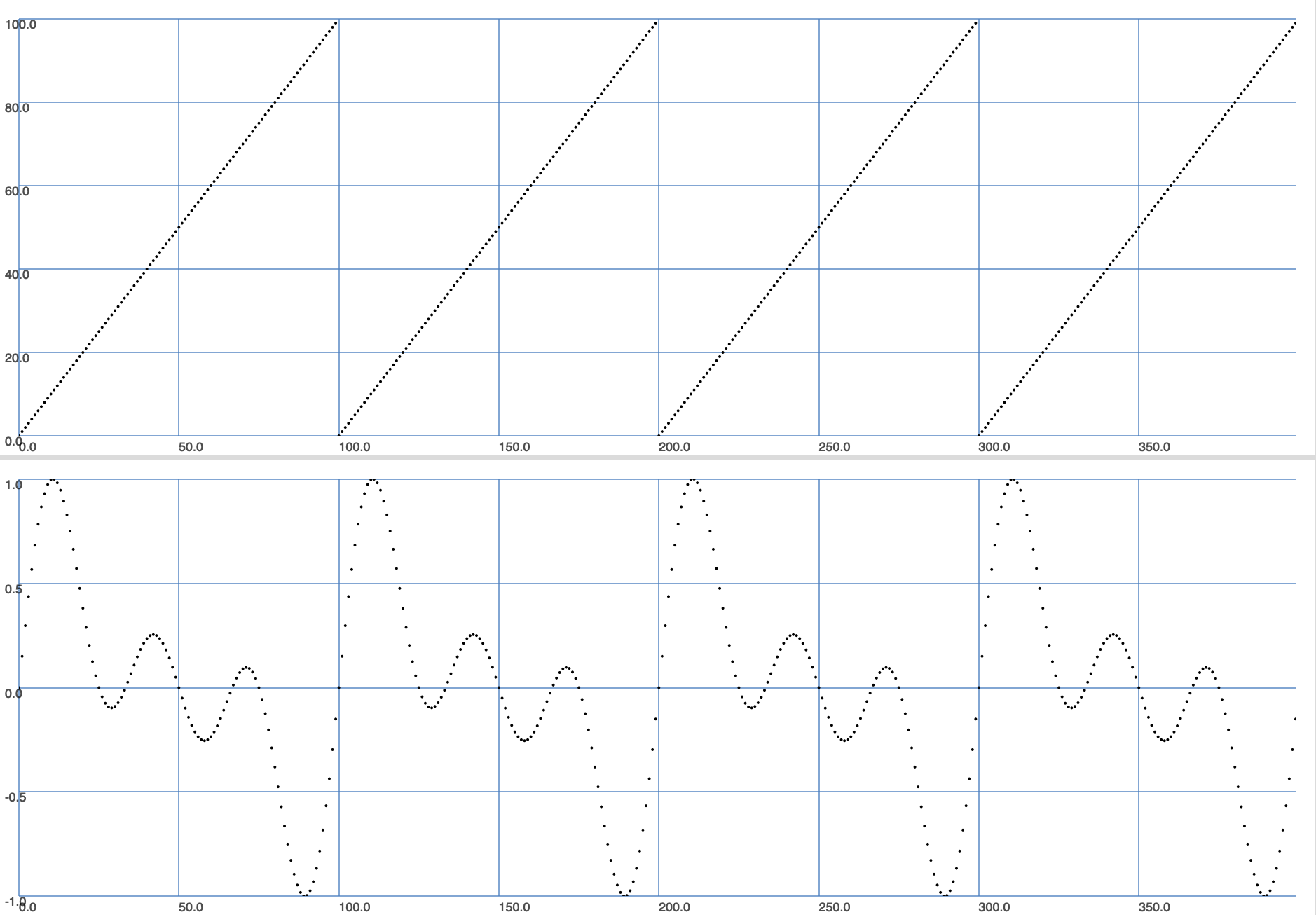
Un periodo del fasore coincide con un periodo della wavetable e dunque la frequenza del fasore (in Hz) determina anche la frequenza dell'oscillatore.
Il timbre stratching rende indipendenti i due periodi ad esempio riducendo del 50% il periodo della wavetable (Duty cycle = 50%).
N.B. La wavetable è sempre di 100 campioni.
from IPython.display import HTML
HTML('<center><img src="media/Stch_1.png" width="55%"></center>')
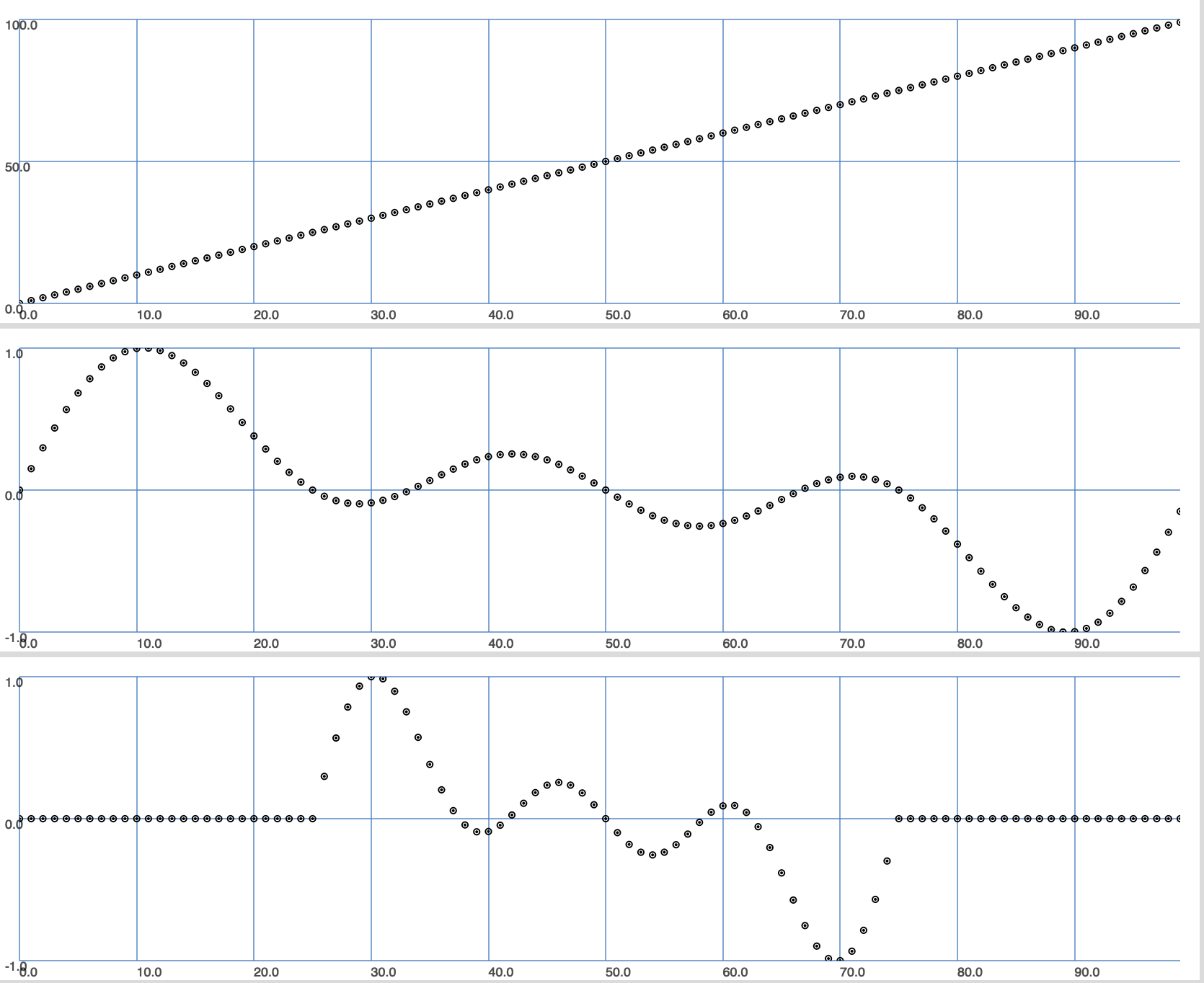
Rileggendo con lo stesso fasore questa nuova wavetable otteniamo il 50% di silenzio tra una rilettura e la successiva della wavetable (lo stretching avviene al centro del periodo per preservare le fasi nel computo della serie di Fourier).
from IPython.display import HTML
HTML('<center><img src="media/Stch_2.png" width="55%"></center>')
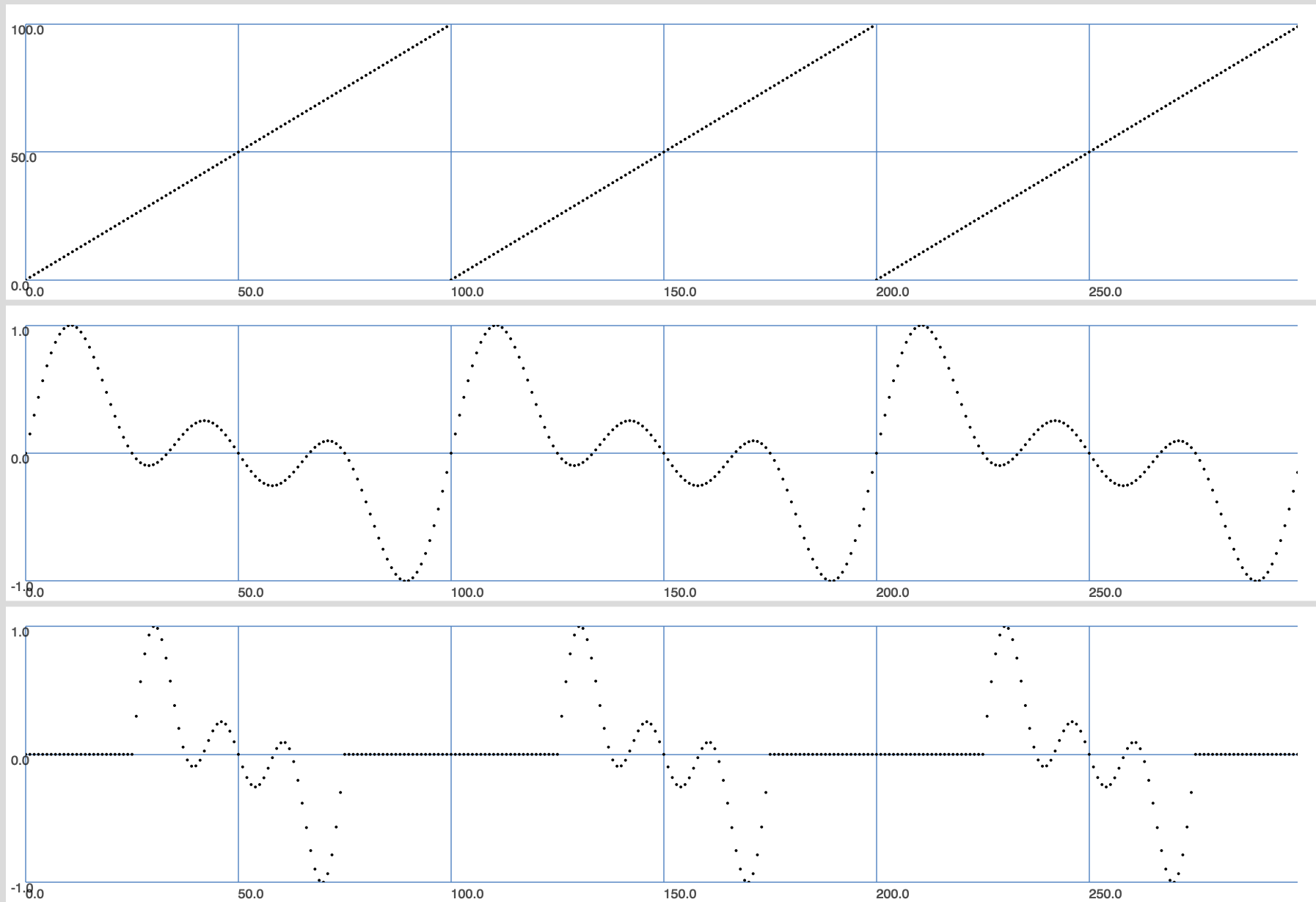
Se:
from IPython.display import HTML
HTML('<center><img src="media/Stch_3.png" width="55%"></center>')
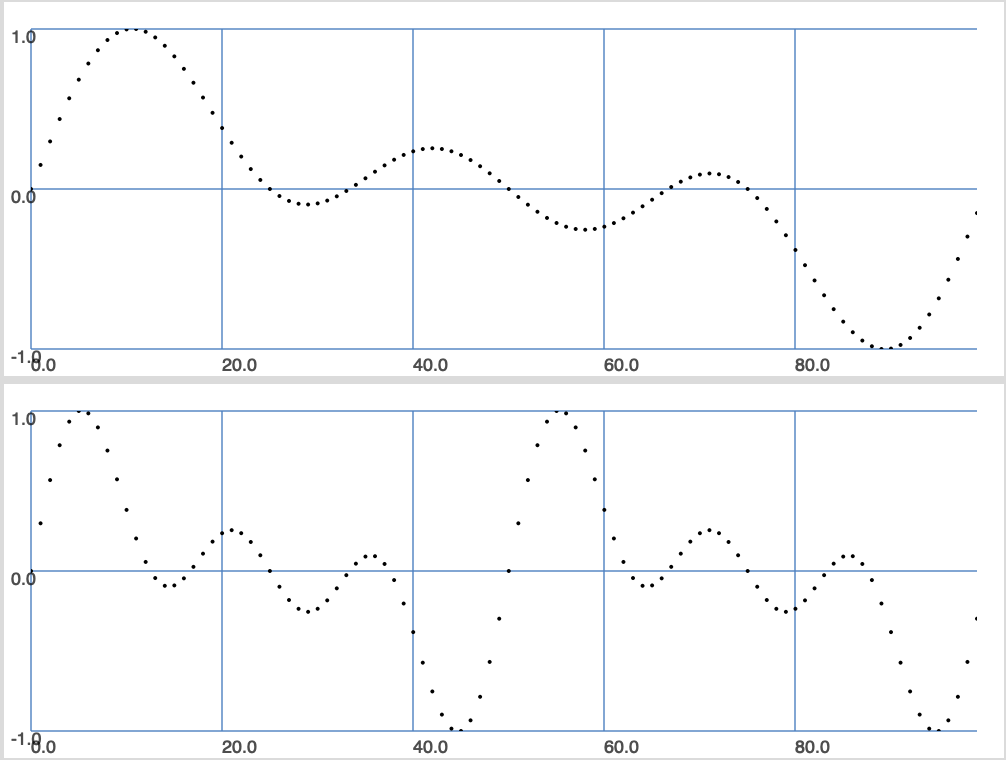
Otteniamo esattamente la forma d'onda originale a frequenza doppia e anche tutti i parziali avranno frequenza doppia.
200 * [1,2,3] * 1; // Frequenze parziali 100% (in Hz)
200 * [1,2,3] * 2; // Frequenze parziali 50% (in Hz)
Ricordando che la frequenza è data dalla velocità angolare la funzione d'onda si trasforma dunque in.
(
p = 100; // 100% Duty cycle
b = p.collect({arg n; (1 * sin(2 * 2pi/p * 1 * n + 0)) + // Primo armonico
(1 * sin(2 * 2pi/p * 2 * n + 0)) + // Secondo armonico
(1 * sin(2 * 2pi/p * 3 * n + 0)) // Terzo armonico
});
b = b.normalize(-1,1);
b.plot(discrete:false);
)
In questo caso (50% duty cycle) i parziali raddoppiati in frequenza dello spettro originale diventano i parziali pari dello spettro risultante mentre per i parziali dispari se la forma d'onda si collega con continuità ad entrambe le estremità dell'asse x si comportano come quelli pari.
//=================================================================
// AUDIO
// Per poter cambiare dinamicamenti il timbro nel tempo (principale
// scopo di questa tecnica) non possiamo utilizzare due o più
// wavetables di size differente (o riscrivere la stessa dinamicamente)
// ma possiamo sfruttare il CLIPPING che si viene a creare quando
// richiamiamo INDICI minori di 0 oppure maggiori del size-1 di una
// wavetable. Ecco un esempio esemplificativo relizzato con un Array
// al posto della wavetable:
a = [0.5,0.7,0.9]; // Ampiezze istantanee
// 0 1 2 Indici
a.size; // size = 3
a.at(-2); // clippato (nil)
a.at(-1); // clippato (nil)
//--------------------------
a.at(0);
a.at(1);
a.at(2); // size - 1
//--------------------------
a.at(3); // clippato (nil)
a.at(4); // clippato (nil)
// Dobbiamo RISCALARE il FASORE utilizzato per il wavetable lookup
// NON in un range compreso tra 0 e size-1 della wavetable, MA
// in uno compreso tra:
// INDICI NEGATIVI (che essendo clippati produrranno ampiezze = 0) e
// INDICI MAGGIORI del size della wavetable.
from IPython.display import HTML
HTML('<center><img src="media/Stch_4.png" width="55%"></center>')
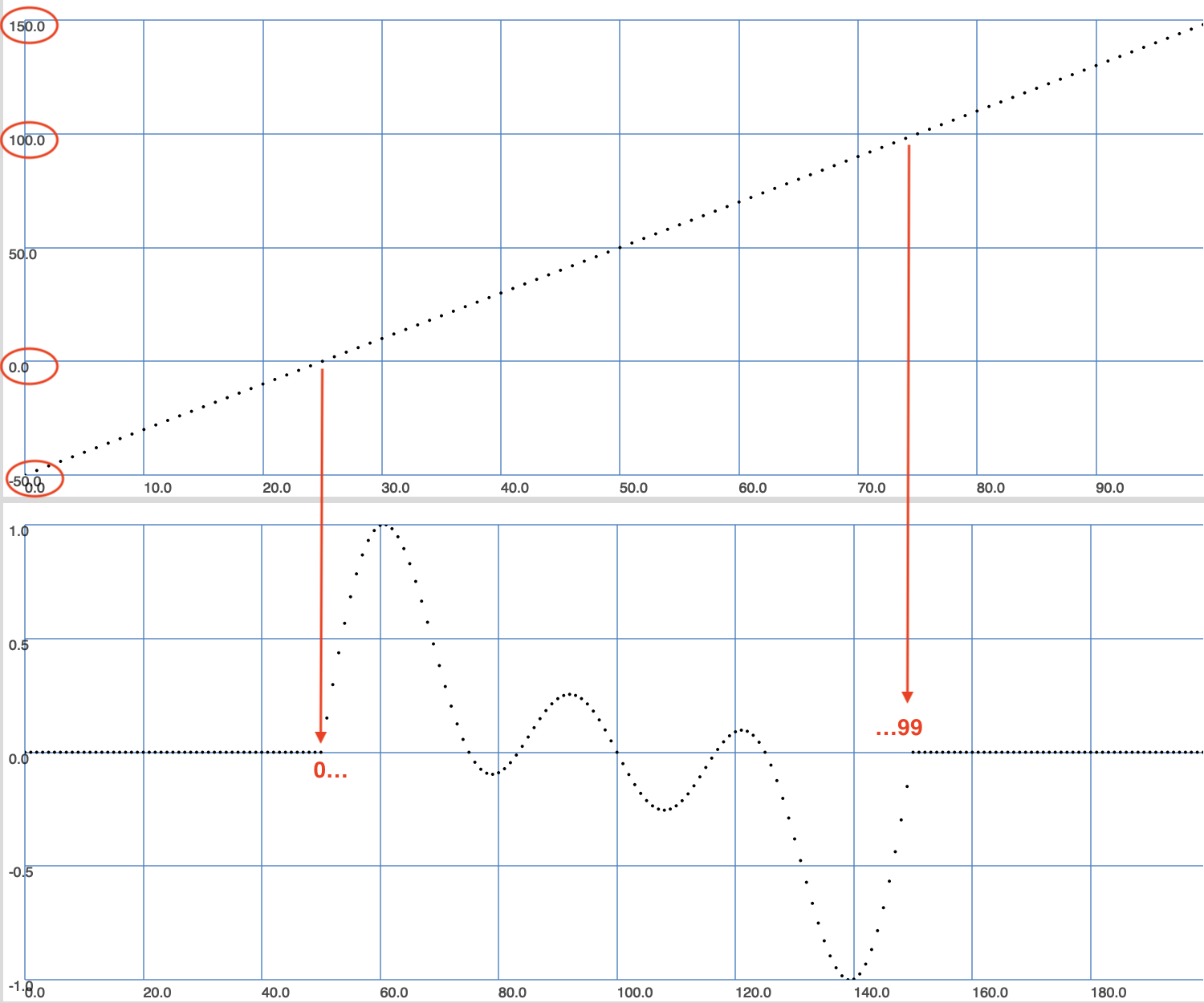
//-----------------------------------------------------------------
// Con BufRd.ar()
// Creiamo un Buffer NON in wavetable format (per questa tecnica
// dobbiamo utilizzare la UGen BufRD.ar() e non Osc.ar()).
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
(
Buffer.freeAll;
b = Buffer.alloc(s, 1024); // Buffer di 1024 samples (p)
b.sine1([1,1,1],true,false); // Funzione d'onda
b.plot;
)
// Siccome il FASORE che andiamo ad utilizzare (LFSaw.ar() è BIPOLARE
// (tra -1 e +1) dobbiamo moltiplicare l'output * 0.5 ottenendo un
// range compreso tra -0.5 e + 0.5 che corrisponde a quanto calcolato
// a RIGA 161. Le operazioni successive sono concatenate in un'unica
// espressione...
{LFSaw.ar}.plot;
(
SynthDef(\stch_1, {arg buf=b, freq=500, f=1,amp=0,gate=0,pan=0,done=0,int=1;
var p,c,sig,env,pann;
p = BufFrames.kr(buf); // Wavetable size (p)
c = LFSaw.ar(freq) * 0.5 * p * f + (p * 0.5); // Fasore Bipolare (a)
sig = BufRd.ar(1,buf,c,1,int);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
a = Synth(\stch_1, [\buf,b,\freq,400,\f,1,\amp,1,\int,4,\done,2,\gate,1]);
// 200*[1,2,3] * 1;
a.set(\f,2); // 200*[1,2,3] * 2;
a.set(\f,3); // 200*[1,2,3] * 3;
a.set(\f,4); // etc
a.set(\f,5);
a.set(\f,6);
a.set(\f,7);
a.set(\f,8);
a.set(\f,9);
a.set(\f,10);
a.set(\gate,0);
//-----------------------------------------------------------------
// Spettri complessi
//
// Generiamo una wavetables con un'onda a dente di sega limitata in
// frequenza (Tutti gli armonici con ampiezze decrescenti 1/num_harm)
(
Buffer.freeAll;
b = Buffer.alloc(s, 1024); // Buffer di 1024 samples (p)
~punti = 512; // Numero di punti (size della tavola)
~npar = 45; // Numero di parziali
~harm = ~npar.collect({arg n; n}); // Tutti gli armonici (da 0)
~sign = -1**~harm; // Segno alternato
~amps = 1.0/(1+~harm*~sign); // Ampiezze decrescenti
b.sine1(~amps,true,false); // Funzione d'onda
b.plot;
)
// Programmiamo un Synth dove possiamo controllare il FATTORE di
// stretching dinamicamente attraverso la posizione del Mouse
// sull'asse y dello schermo in un range compreso tra 1 (100% duty
// cycle) e 100 (1% duty cycle). Possiamo vedere i valori nella Post
// Window grazie al metodo '.poll'
(
SynthDef(\stch_2, {arg buf=b,freq=500,amp=0,gate=0,pan=0,done=0,int=1;
var p,f,c,sig,env,pann;
p = BufFrames.kr(buf); // Wavetable size (p)
f = MouseY.kr(1,10).poll; // Stretching factor
c = LFSaw.ar(freq) * 0.5 * p * f + (p * 0.5); // Fasore Bipolare (a)
sig = BufRd.ar(1,buf,c,1,int);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
a = Synth(\stch_2, [\buf,b,\freq,400,\amp,1,\int,4,\done,2,\gate,1]);
a.release;
// Come possimo notare MUOVENDO IL MOUSE:
//
// • Nel passaggio DINAMICO tra un numero intero e il successivo
// come fattori di stretching si viene a creare una sorta di
// "CROSSFADE" tra gli armonici.
//
// • All'AUMENTARE del FATTORE di STRETCHING lo spettro si APPIATTISCE
// verso l'alto ovvero AUMENTANO le ampiezze delle FREQUENZE ACUTE
// (e la serie di Fourier si allunga dello stesso fattore) e
// DIMINUISCONO quelle delle FREQUENZE GRAVI.
//-----------------------------------------------------------------
// Mapping parametri
// Un solo valore controlla il timbro...due (quattro) possibilità
// di controllo.
// -------> 1) Timbro mappato argomenti
a = Synth(\stch_1, [\buf,b,\freq,400,\f,1,\amp,1,\int,4,\done,2,\gate,1]);
a.set(\f,rrand(1.0,10).postln);
(
r = Routine.new({
inf.do({
a.set(\f,rrand(1.0,10).postln);
0.1.wait;
})
}).play
)
r.stop;
a.set(\gate,0)
// -------> 2) Timbro mappato su segnale di controllo esterno
// Trovare il range che ci aggrada...
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(1.8,1.87).poll(10); // Trovare il range che interessa
Out.kr(busOut,sig)
}).add;
{m = Synth(\mouse, [\busOut, ~mouseY])}.defer(1); // Synth per ksig
a = Synth(\stch_1, [\buf,b,\freq,400,\f,~mouseY.asMap,\amp,1,\int,4,\done,2,\gate,1],s,\addToTail);
)
// -------> 3) Timbro mappato sull'inviluppo d'ampiezza
// Trovare il range che ci aggrada...
(
SynthDef(\stch_3, {arg buf=b,freq=500,amp=0,dur=1,t_gate=0,pan=0,done=0,int=1;
var p,bpf,env,f,c,sig,pann;
p = BufFrames.kr(buf);
bpf = Env.perc(0.01,dur-0.01);
env = EnvGen.kr(bpf,t_gate,doneAction:done);
f = env.linlin(0,1,1,1.001).poll; // Inviluppo riscalato
c = LFSaw.ar(freq) * 0.5 * p * f + (p * 0.5);
sig = BufRd.ar(1,buf,c,1,int);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
Synth(\stch_3, [\buf,b,\freq,rrand(50,62).midicps,\amp,rand(1.0),\dur,1.5,\int,4,\done,2,\t_gate,1]);
// -------> 4) Timbro mappato su segnale di controllo interno
// Con chorusing...
(
SynthDef(\stch_4, {arg buf=b,freq=500,freqT=0.1,amp=0,gate=0,pan=0,done=0,int=1;
var p,f,c,sig,env,pann;
p = BufFrames.kr(buf);
f = LFNoise1.kr(freqT ).range(1.35,1.8).poll;
c = LFSaw.ar([freq,freq+0.5]) * 0.5 * p * f + (p * 0.5);
sig = BufRd.ar(1,buf,c,1,int);
env = Linen.kr(gate,doneAction:done);
pann = Pan2.ar(sig*amp*env,pan);
Out.ar(0,pann)}
).add;
)
a = Synth(\stch_4, [\buf,b,\freq,200,\freqT,1,\amp,0.3,\int,4,\done,2,\gate,1]);
a.release;
//=================================================================
// Funzioni d'onda
// Attraverso una funzione d'onda possiamo scrivere tutti i valori
// di AMPIEZZA ISTANTANEA relativi a un CICLO di ONDA PERIODICA
// per poi rileggerli attraverso OSCILLATORI TABELLARI.
//
// f[n] = a * sin(w * n + O) --> Funzione della sinusoide
(
~punti = 100; // Numero di punti (size della tavola)
~freq = 1; // Numero di cicli per size della tavola
~amp = 1.0; // Ampiezza di picco
~w = 2pi/(~punti/~freq); // Calcolo della velocità angolare (rad/sec)
p = ~punti.collect({arg n; ~amp * sin(~w * n + 2pi)}); // n assume ad ogni valutazione
// l'indice dell'Array
// partendo da 0
p.plot(minval: -1, maxval:1,discrete:true); // Visualizza
)
//-----------------------------------------------------------------
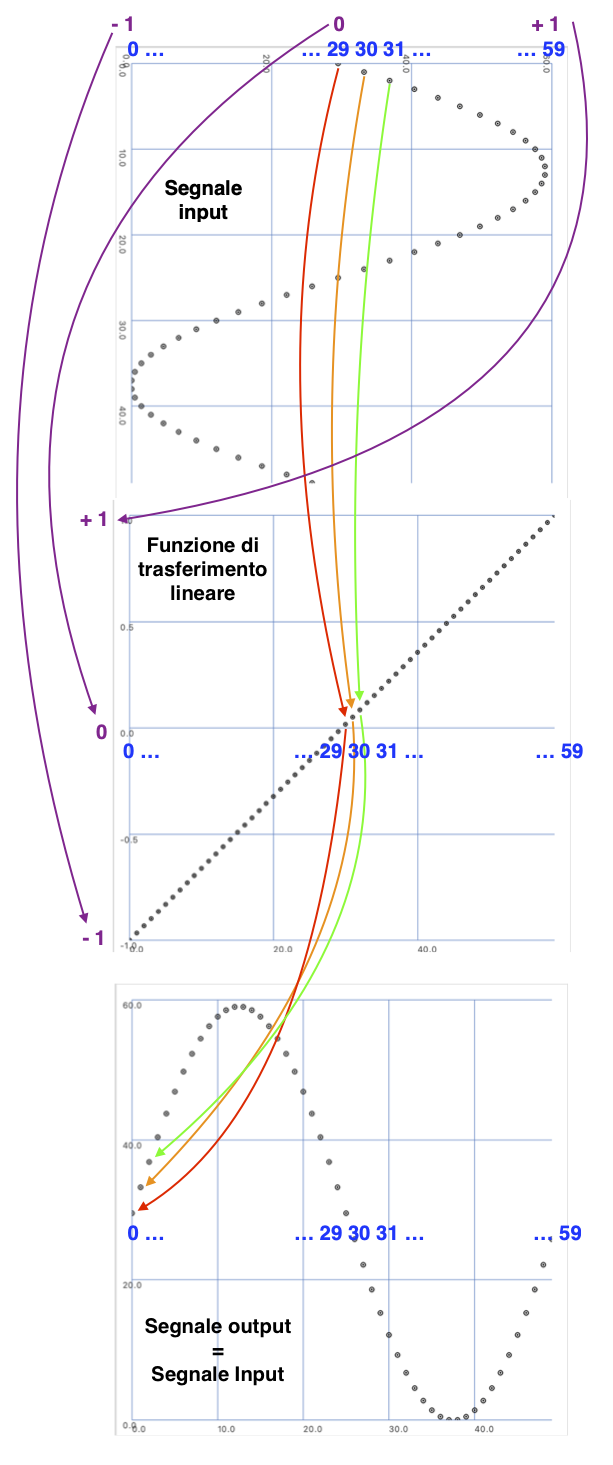
// Funzioni di trasferimento (Transfer function)
// Una funzione di trasferimento caratterizza il comportamento di
// un SISTEMA DINAMICO TEMPO INVARIANTE mettendo in relazione un
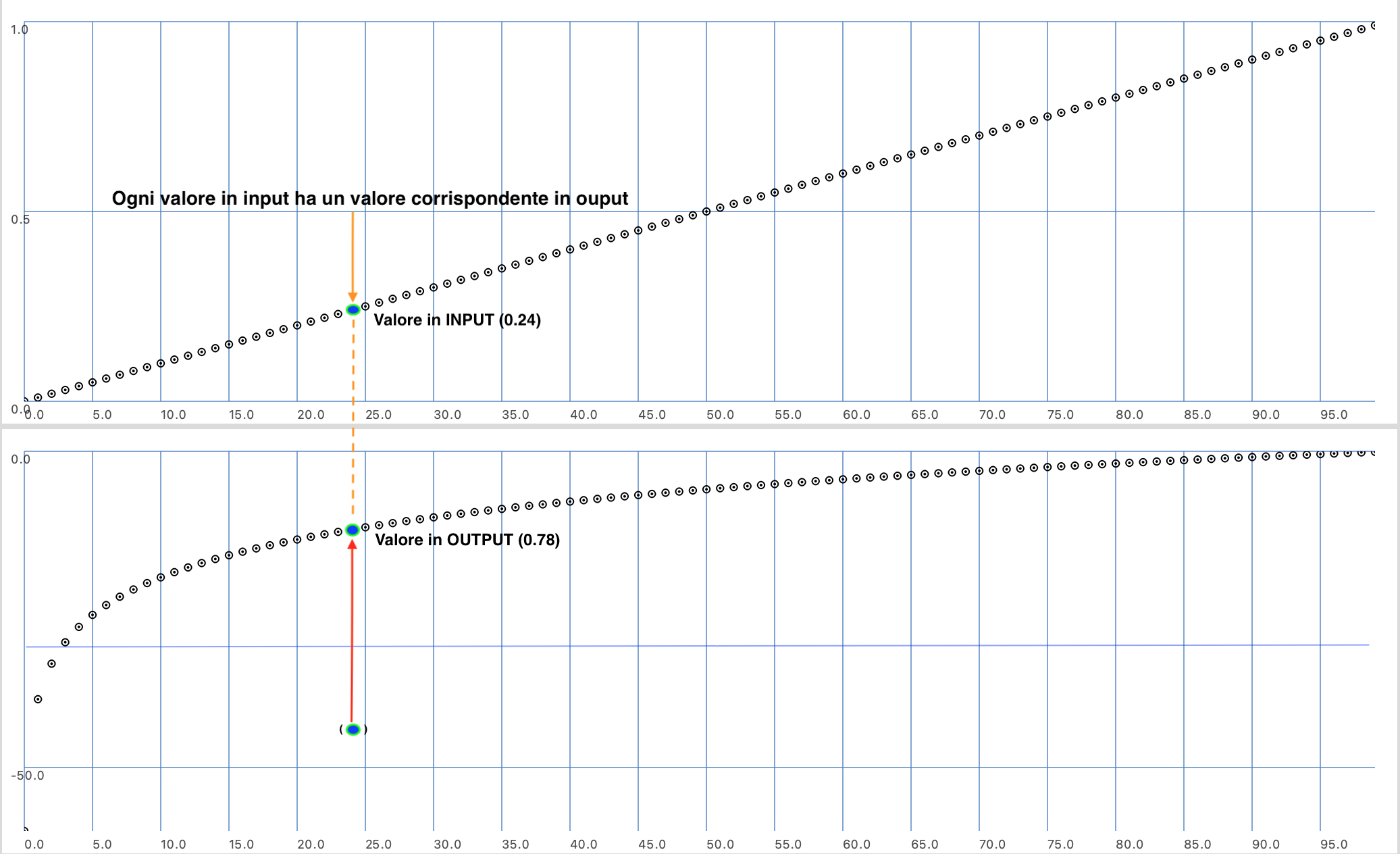
// valore in INPUT con un valore in OUTPUT.
//
// Prendiamo come esempio la formule di CONVERSIONE tra AMPIEZZA
//
// LINEARE e DECIBEL:
//
// dB[n] = 20 * log[10](n/1) --> Transfer function da lin a dB
~punti = 100; // Numero di punti della tavola
~lin = ~punti.collect({arg n; n/100}); // Rampa lineare tra 0 e 1
// Prendiamo come valori in INPUT (n) della funzione la rampa lineare
// tra 0 e 1 e PER OGNI VALORE uno dopo l'altro applichiamo la
// FUNZIONE DI TRASFERIMENTO:
~db = ~lin.collect({arg n; 20*log10(n+0.001)/1.0});
// N.B. Abbiamo aggiunto + 0.001 in quanto con 0 questa funzione
// restituisce -inf e non potremmo visualizzarlo in un plotter.
[~lin,~db].plot(discrete:true); // Visualizza INPUT (lineare) e OUTPUT (dB)
from IPython.display import HTML
HTML('<center><img src="media/T_func.png" width="80%"></center>')
from IPython.display import HTML
HTML('<center><img src="media/wave_1.png" width="40%"></center>')
from IPython.display import HTML
HTML('<center><img src="media/wave_2.png" width="40%"></center>')
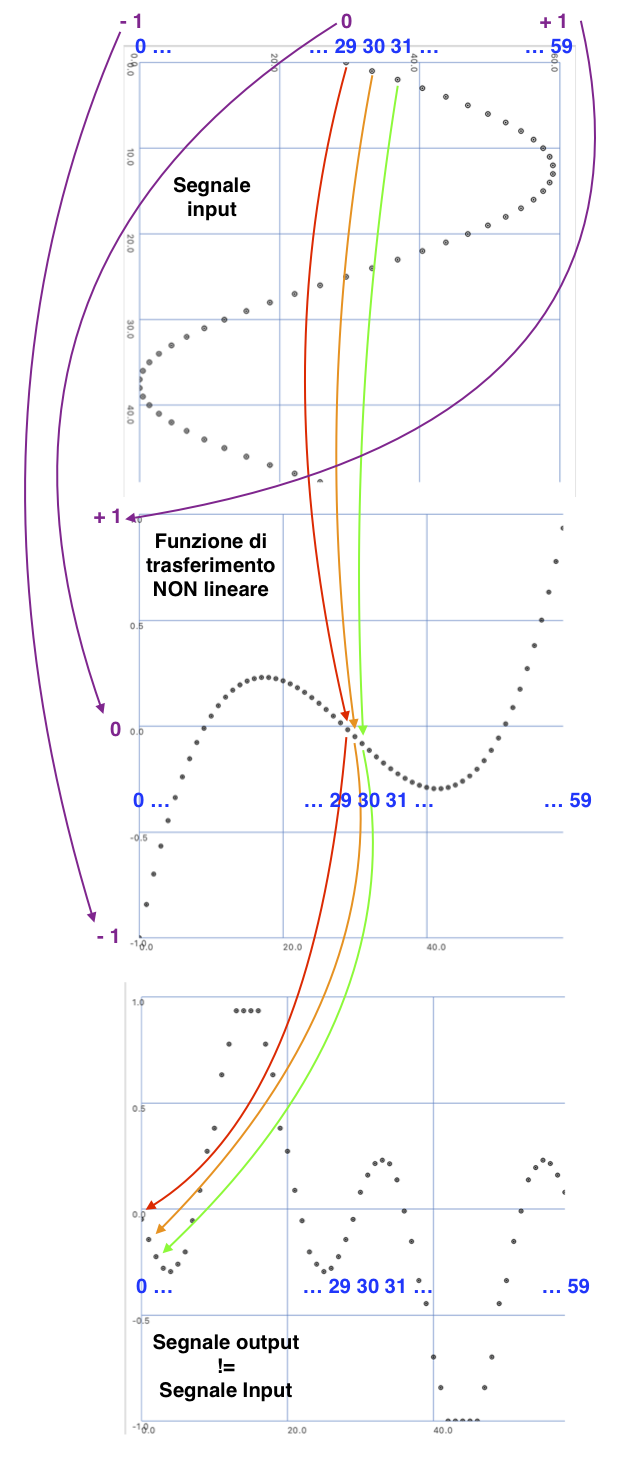
//=================================================================
// In SC Possiamo applicare funzioni di trasferimento direttamente
// sui valori di ampiezza istantanea in uscita da una UGen.
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
//-----------------------------------------------------------------
// Clipping
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\wsh_1, {arg freq=400,amp=0,clip=1,gate=0,pan=0,done=2;
var sig, env;
sig = SinOsc.ar(freq);
sig = sig.clip2(clip); // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(1,0);
Out.kr(busOut,sig)
}).add;
)
(
m = Synth(\mouse, [\busOut, ~mouseY]); // Synth per ksig
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
)
a.set(\clip, 0.1);
a.set(\clip, ~mouseY.asMap);
a.release;
// Se il timbro di un suono è composto dalla somma di più sinusoidi
// a frequenze e ampiezze differenti la distorsione dei parziali non
// sarà uguale per tutti...
(
{var in,amp;
amp = MouseY.kr(0,0.99).poll(10);
in = SinOsc.ar(69.midicps, 0, 0.7*amp) +
SinOsc.ar(73.midicps, 0, 0.2*amp) +
SinOsc.ar(76.midicps, 0,0.1*amp);
in.clip2(0.5);
}.scope;
)
// Parziali in rapporto armonico distorti rafforzano la percezione
// della fondamentale (inesistente...)
(
{var in, amp;
amp = MouseY.kr(0,0.99).poll(10);
in = SinOsc.ar(4*110, 0, amp) +
SinOsc.ar(5*110, 0, amp) +
SinOsc.ar(6*110, 0, amp);
in.clip2(0.5);
}.scope;
)
//-----------------------------------------------------------------
// Minimum
// Clippa solo la parte positiva
12.min(0.5)
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\wsh_1, {arg freq=400,amp=0,clip=1,gate=0,pan=0,done=2;
var sig, env;
sig = SinOsc.ar(freq);
sig = sig.min(clip); // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(1,0);
Out.kr(busOut,sig)
}).add;
)
(
m = Synth(\mouse, [\busOut, ~mouseY]); // Synth per ksig
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
)
a.set(\clip,0.5);
a.set(\clip,~mouseY.asMap);
a.release;
//-----------------------------------------------------------------
// Maximum
// Clippa solo la parte negativa
12.max(0.5)
(
~mouseY = Bus.control(s, 1); // (server, n_canali)
SynthDef.new(\wsh_1, {arg freq=400,amp=0,clip=1,gate=0,pan=0,done=2;
var sig, env;
sig = SinOsc.ar(freq);
sig = sig.max(clip); // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(1,0);
Out.kr(busOut,sig)
}).add;
)
(
m = Synth(\mouse, [\busOut, ~mouseY]); // Synth per ksig
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
)
a.set(\clip,0.5);
a.set(\clip,~mouseY.asMap);
a.release;
//-----------------------------------------------------------------
// Softclip
// Distorce con una regione perfettamente lineare tra -0.5 e 0.5
(
SynthDef.new(\wsh_1, {arg amp=0,gate=0,pan=0,done=2;
var sig, env;
// sig = SinOsc.ar;
sig = SoundIn.ar(0);
sig = sig.softclip; // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
)
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
a.release;
(
a = Signal.sineFill(512,[1]);
[a,a.softclip].plot;
)
//-----------------------------------------------------------------
// Distort
// Distorsione non lineare
(
SynthDef.new(\wsh_1, {arg amp=0,gate=0,pan=0,done=2;
var sig, env;
// sig = SinOsc.ar;
sig = SoundIn.ar(0);
sig = sig.distort; // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
)
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
a.release;
(
a = Signal.sineFill(512,[1]);
[a,a.distort].plot;
)
//-----------------------------------------------------------------
// Squared (quadrato)
// Parte negativa diventa positiva = ottava sopra con DC offset
(
SynthDef.new(\wsh_1, {arg amp=0,gate=0,pan=0,done=2;
var sig, env;
//sig = SinOsc.ar;
sig = SoundIn.ar(0);
sig = sig.squared; // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
)
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
a.release;
(
a = Signal.sineFill(512,[1]);
[a,a.squared*2-1].plot;
)
//-----------------------------------------------------------------
// Cubed
// Fondamentale e terzo armonico...
(
SynthDef.new(\wsh_1, {arg amp=0,gate=0,pan=0,done=2;
var sig, env;
sig = SinOsc.ar;
//sig = SoundIn.ar(0);
sig = sig.cubed; // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
)
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
a.release;
(
a = Signal.sineFill(512,[1]);
[a,a.cubed].plot;
)
//-----------------------------------------------------------------
// Square root (Radice quadrata)
// Spettro dell'onda triangolare
(
SynthDef.new(\wsh_1, {arg amp=0,gate=0,pan=0,done=2;
var sig, env;
sig = SinOsc.ar;
//sig = SoundIn.ar(0);
sig = sig.sqrt; // Funzione di trasferimento
sig = LeakDC.ar(sig); // Rimuove DC offset
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig * env * amp, pan);
Out.ar(0,sig);
}).add;
)
a = Synth.new(\wsh_1, [\amp,0.5,\gate,1],s,\addToTail); // Synth per out
a.release;
(
a = Signal.sineFill(512,[1]);
[a,a.sqrt].plot;
)
//=================================================================
// Un'altra tecnica che possimo utilizzare consiste nel memorizzare
// la tranfer function in un Buffer e rileggerla con Shaper.ar()
(
Buffer.freeAll;
~punti = 1024;
~clip1 = Signal.newClear(~punti);
~clip1.waveFill({arg x; x},-1, 1); // Rampa lineare tra -1 e +1
~clip1 = ~clip1.clip2(0.5); // Tranfert Funcion
b = Buffer.loadCollection(s,~clip1.asWavetableNoWrap); // Non ottimizzato per il wrap around...
{b.plot(minval:-1,maxval:1)}.defer(1);
)
(
SynthDef.new(\wsh, {arg buf=b,freq=400,shp=0,amp=0,gate=0,pan=0,done=2;
var sig, sigIn, env;
sigIn = SinOsc.ar(freq) * shp;
sig = Shaper.ar(buf, sigIn);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*env*amp,pan);
sig = LeakDC.ar(sig);
Out.ar(0,sig)
}).add;
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(0,1).poll(10);
Out.kr(busOut,sig)
}).add;
~mouseY = Bus.control(s, 1); // (server, n_canali)
{Synth(\mouse, [\busOut, ~mouseY])}.defer(1);
)
a = Synth.new(\wsh, [\buf,b,\freq,400,\shp,1,\amp,0.2,\gate,1],s,\addToTail);
a.set(\shp,0.5);
a.set(\shp, ~mouseY.asMap);
a.free;
from IPython.display import HTML
HTML('<center><img src="media/Chebi.png" width="35%"></center>')
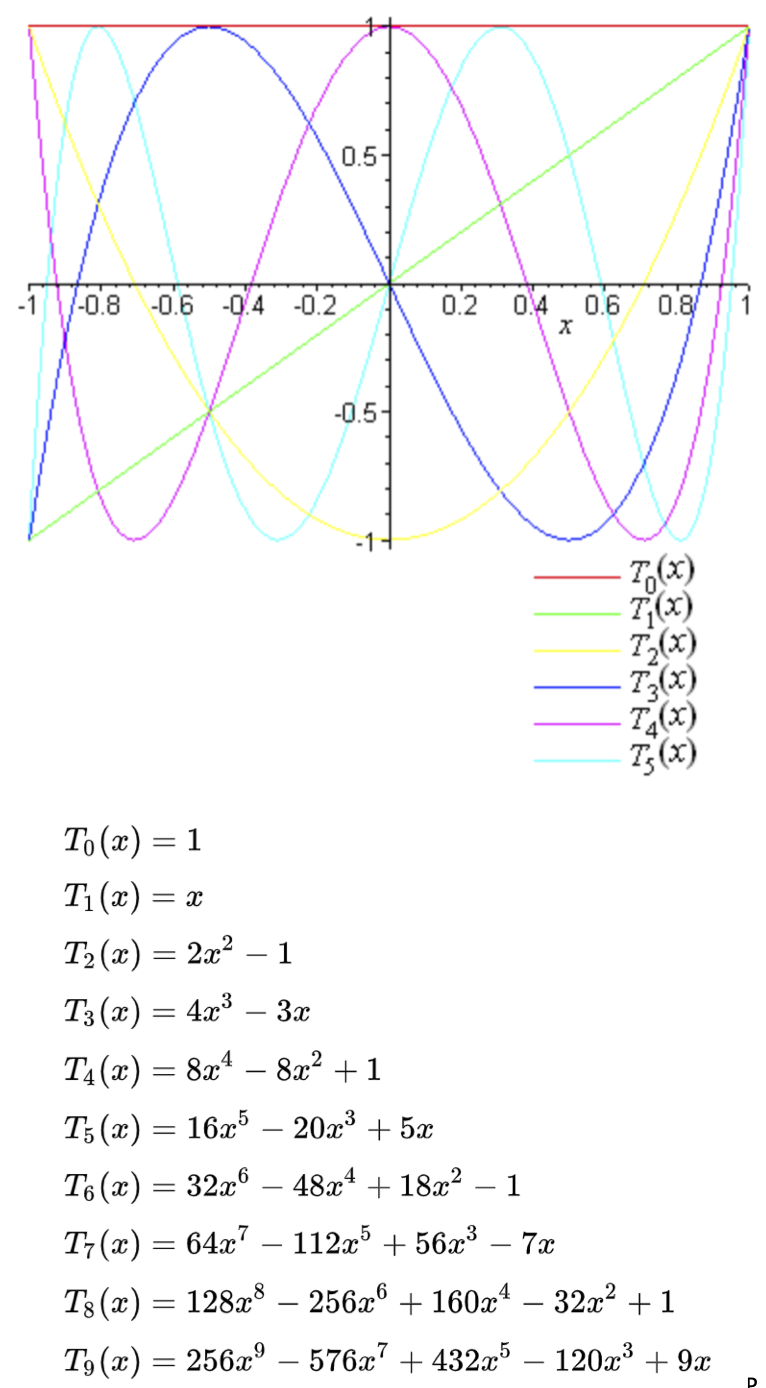
//=================================================================
// Funzione di trasferimento Polinomi di Chebyshev di prima specie
// T0[n] = 1
// T1[n] = n
// T2[n] = 2n**2 - 1
// T3[n] = 4n**3 - 3n
// T4[n] = 8n**4 - 8n**2 + 1
// T5[n] = 16n**5 - 20n**3 + 5n
// ...
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
(
Buffer.freeAll;
SynthDef.new(\wsh, {arg buf=b,freq=400,shp=0,amp=0,gate=0,pan=0,done=2;
var sig, sigIn, env;
sigIn = SinOsc.ar(freq) * shp;
sig = Shaper.ar(buf, sigIn);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*env*amp,pan);
sig = LeakDC.ar(sig);
Out.ar(0,sig)
}).add;
SynthDef.new(\mouse, {arg busOut=0;
var sig;
sig = MouseY.kr(0,1);
Out.kr(busOut,sig)
}).add;
~mouseY = Bus.control(s, 1); // (server, n_canali)
{Synth(\mouse, [\busOut, ~mouseY])}.defer(1);
)
~punti = 512; // Numero di punti della tavola
~lin = ~punti.collect({arg n; n/256-1}); // Rampa lineare tra -1 e 1
~lin.plot(bounds:600@400, minval: -1, maxval:1,discrete:true);
//------------------------------------------------------------------
// T1[n] = n
// Primo armonico
~cheb1 = ~lin.collect({arg n; n})
~cheb1.plot(bounds:600@400, minval: -1, maxval:1,discrete:true);
// Ampiezza primo armonico (lineare)
a = Signal.chebyFill(~punti, [1], zeroOffset: true, normalize: true);
a.asWavetable;
b = Buffer.loadCollection(s,a);
b.free;
b = Buffer.alloc(s,~punti);
b.cheby([1],true,true,true); // amps, normalize, asWavetable, clearFirst
b.plot(bounds:600@400, minval: -1, maxval:1);
a = Synth.new(\wsh, [\buf,b,\freq,400,\shp,1,\amp,0.2,\gate,1],s,\addToTail);
a.set(\shp,0.5);
a.set(\shp, ~mouseY.asMap);
a.free;
//------------------------------------------------------------------
// T2[n] = 2n**2 - 1
// Secondo armonico
~cheb2 = ~lin.collect({arg n; 2*(n**2) - 1})
~cheb2.plot(bounds:600@400, minval: -1, maxval:1,discrete:true);
b.free;
b = Buffer.alloc(s,~punti);
b.cheby([1,1],true,true,true); // amps, normalize, asWavetable, clearFirst
b.plot(bounds:600@400, minval: -1, maxval:1);
a = Synth.new(\wsh, [\buf,b,\freq,400,\shp,1,\amp,0.2,\gate,1],s,\addToTail);
a.set(\shp,0.5);
a.set(\shp, ~mouseY.asMap);
a.free;
// N.B. Notiamo la differenza tra la funzione calcolata punto per
// punto e la stessa realizzata con Signal.chebyFill:
// • la prima va da -1 a + 1
// • la seconda va da 0 a 1
// Questo perchè nella seconda l'argomento zeroOffset è settato su
// 'true' e fa sì che il punto al centro della tavola dal quale
// comincia la lettura cominci da 0 senza discontinuità (click)
// alla lettura del primo ciclo.
//------------------------------------------------------------------
// T3[n] = 4n**3 - 3n
// Terzo armonico
b = Buffer.alloc(s,~punti);
b.cheby([0,0,1],true,true,true);
b.plot(bounds:600@400, minval: -1, maxval:1);
//------------------------------------------------------------------
// T4[n] = 8n**4 - 8n**2 + 1
// Quarto armonico
b = Buffer.alloc(s,~punti);
b.cheby([0,0,0,1],true,true,true);
b.plot(bounds:600@400, minval: -1, maxval:1);
//------------------------------------------------------------------
// T5[n] = 16n**5 - 20n**3 + 5n
// Quinto armonico
b = Buffer.alloc(s,~punti);
b.cheby([0,0,0,0,1],true,true,true);
b.plot(bounds:600@400, minval: -1, maxval:1);
//------------------------------------------------------------------
// Sintesi Additiva a spettro variabile
b.free;
b = Buffer.alloc(s,~punti);
b.cheby([1,0.2,0.7,0.3,1],true,true,true);
b.plot(bounds:600@400, minval: -1, maxval:1);
a = Synth.new(\wsh, [\buf,b,\freq,400,\shp,1,\amp,0.2,\gate,1],s,\addToTail);
a.set(\shp,0.5);
a.set(\shp, ~mouseY.asMap);
a.free;
// Partiamo dal principio del Wavetable Lookup.
// Possiamo computare i valori y di una wavetable bidimensionale
// attraverso una funzione d'onda
// UNA VARIABILE: wave(x)
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
//------------------------------------------------------------------
// 1_WTS
// f[x] = sin(x) --> x tra 0 e 2pi (angolo giro)
(
f = {arg x; sin(x)}; // Funzione d'onda
SynthDef.new(\wts_1, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs, sig, env;
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Fasore da 0 a 2pi (angolo giro)
sig = Limiter.ar( f.value(phs) ); // Valuta la funzione ad audio rate
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_1,[\amp,0.2,\gate,1])
a.release;
Se definiamo una wavetable tridimensionale attraverso una funzione d'onda a due variabili: wave(x[n], y[n]) possiamo rappresentarla come una superficie tridimensionale chiamandola Wave Terrain (WT).
from IPython.display import HTML
HTML('<center><img src="media/WT_1.png" width="50%"></center>')
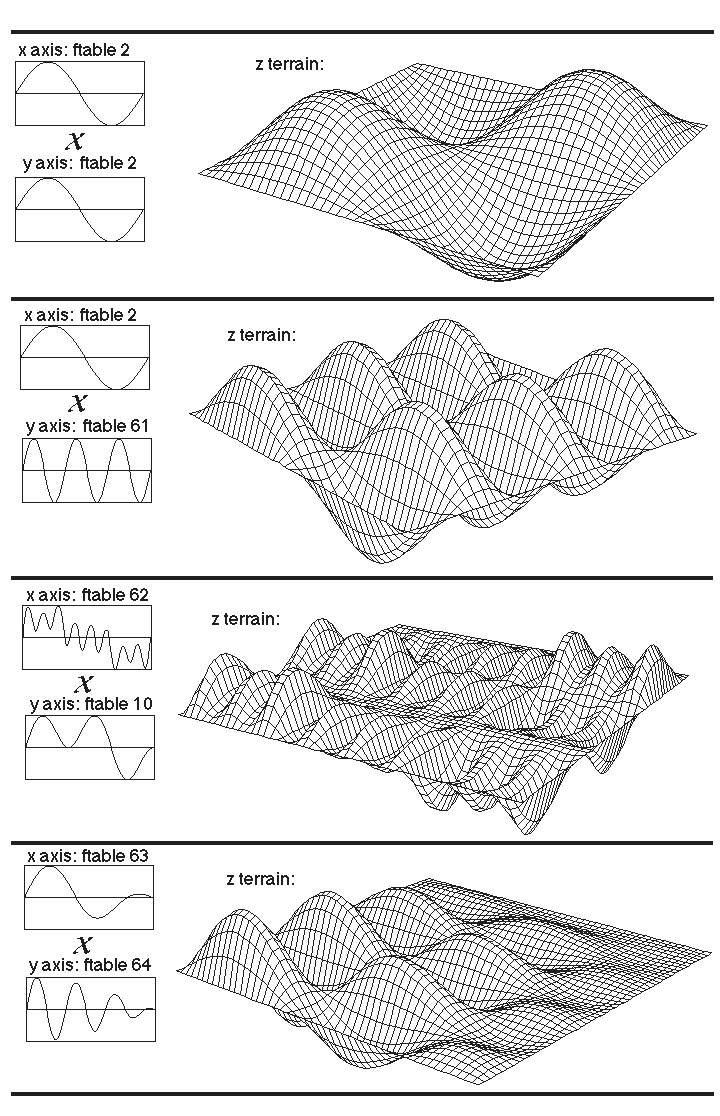
Le ampiezze istantanee (valori y nel wavetable lookup bidimensionale) corrispondono all'altezza della figura (valori z).
from IPython.display import HTML
HTML('<center><img src="media/WT_0.png" width="35%"></center>')
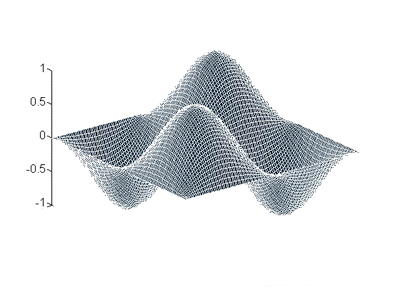
Questi valori possono essere richiamati attraverso non uno ma due indici (x, y) come qualsiasi punto su di un asse cartesiano.
from IPython.display import HTML
HTML('<center><img src="media/WT_2.png" width="40%"></center>')
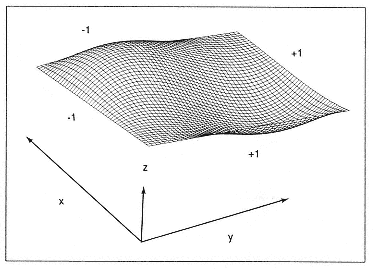
from IPython.display import HTML
HTML('<center><img src="media/Orbita_1.png" width="45%"></center>')
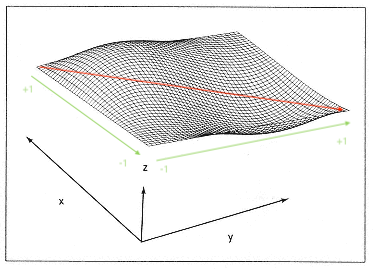
// 2_Orbita_lineare
(
// Funzione con x e y...
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_2, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs, x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1); // Tra -1 e +1
x = phs * -1; // Tra +1 e -1
y = phs;
[x,y].scope; // Metti visualizzazione XY
// ------------------------------
sig = Limiter.ar( f.value(x, y) ); // Valuta la funzione ad audio rate
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_2,[\amp,0.2,\gate,1])
a.set(\freq,200)
a.release;
from IPython.display import HTML
HTML('<center><img src="media/Orbita_2.png" width="45%"></center>')
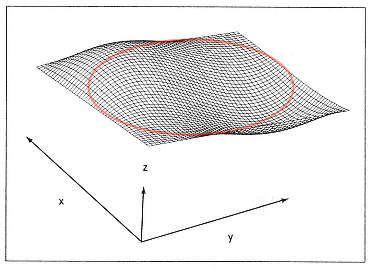
// 3_Orbita_circolare
//
// Nel caso precedente la superficie è letta in modo diagonale (vedi WT_2.png)
// ma possiamo "esplorare" la superfice in qualsiasi modo. Queste
// esplorazioni si chiamano ORBITE e descrivono una sequenza di punti
// sulla superficie nel tempo.
// Ad esempio basterà calcolare il seno e il
// coseno del segnale lineare per delineare un'orbita circolare ottenendo
// uno spettro differente (vedi WT_3.png):
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs, x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
x = sin(phs);
y = cos(phs);
[x,y].scope; // Metti visualizzazione XY
// ------------------------------
sig = Limiter.ar(f.value(x, y)); // Valuta la funzione ad audio rate
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.release;
from IPython.display import HTML
HTML('<center><img src="media/Orbita_3.png" width="35%"></center>')
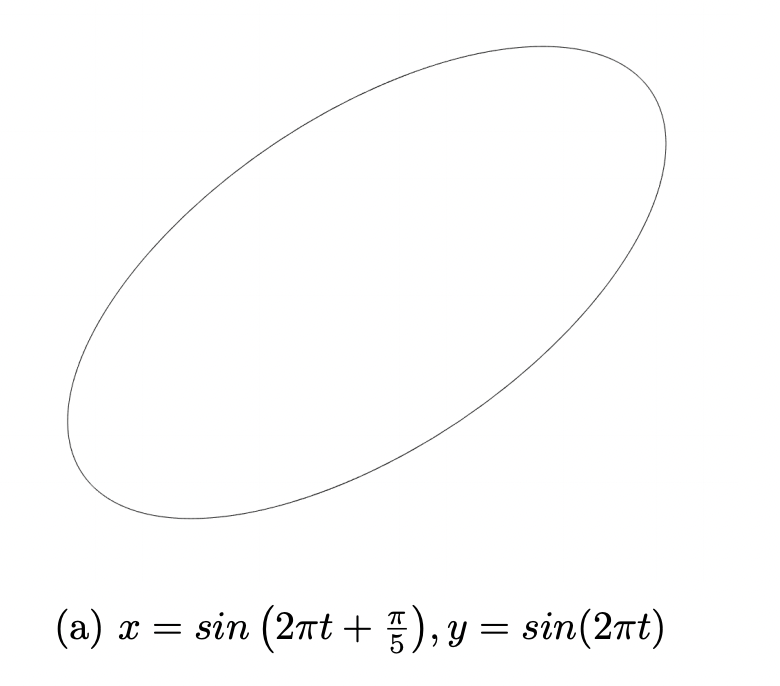
// 4_Orbita_ellittica
// Oppure sfasare dinamicamente y per ottenere ellissi...
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs,offph, x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
offph = MouseY.kr(0,pi); // Defasaggio
//offph = Line.ar(0,pi,5);
x = sin(phs);
y = sin(phs + offph);
[x,y].scope;
// ------------------------------
sig = Limiter.ar(f.value(x, y));
sig = LeakDC.ar(sig);
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.release;
Possiamo modificare dinamicamente il raggio dell'orbita con un fattore di moltiplicazione compreso tra 0.0 e 1.0.
from IPython.display import HTML
HTML('<center><img src="media/Raggio.png" width="45%"></center>')
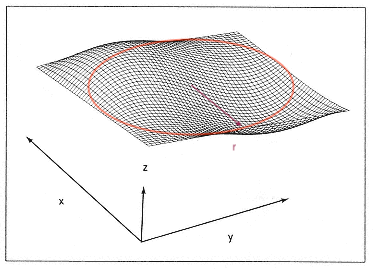
// Raggio
// Possiamo anche cambiare dinamicamente il raggio dell'orbita con un
// fattore di moltiplicazione compreso tra 0.0 e 1.0
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs,r,offph, x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = MouseY.kr(0, 1); // Raggio
offph = MouseX.kr(0,pi); // Defasaggio
x = r * sin(phs);
y = r * sin(phs + offph);
[x,y].scope;
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.release;
Possiamo traslare l'origine sia di x che di y:
// Origine
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs,r,offph, cx,cy,x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = MouseY.kr(0, 1); // Raggio
offph = MouseX.kr(0,pi); // Defasaggio
cx = MouseX.kr(-1, 1.0); // Origine x
cy = MouseY.kr(-1, 1.0); // Origine y
x = r * sin(phs) + cx;
y = r * cos(phs + offph) + cy;
[x,y].scope;
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.release;
// In questo caso la posizione del mouse "esplora" punti diversi della
// superfcie..
from IPython.display import HTML
HTML('<center><img src="media/Lissa.png" width="25%"></center>')
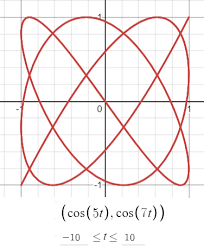
// 5_Lissajous
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg xfreq=110, fratio = #[1,2], offph=0.25,
xpos= 0, xdim=1, ypos= 0, ydim= 1,
amp=0.2,gate=0,pan=0,done=2;
var yfreq, xphs, yphs, xmin, xmax, ymin, ymax, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
yfreq = xfreq * (fratio[0] / fratio[1]); // Calcola la frequenza di y
xphs = LFSaw.ar(xfreq, -1).range(0, 2pi);
yphs = LFSaw.ar(yfreq, -1).range(0, 2pi);
xmin = xpos - xdim;
xmax = xpos + xdim;
ymin = ypos - ydim;
ymax = ypos + ydim;
x = Wrap.ar(sin(xphs),-1,1).range(xmin,xmax);
y = Wrap.ar(sin(yphs + offph),-1,1).range(ymin,ymax);
[x,y].scope; // Metti visualizzazione XY
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.set(\fratio,[rrand(1,10.0),rrand(1,10.0)],\xpos,0,\xdim,1,\ypos,0,\ydim,1);
a.set(\xpos,rand(1.0),\xdim,rand(1.0),\ypos,rand(1.0).postln,\ydim,rand(1.0));
a.release;
// Provare a mappare dei segnali sui parametri pos e dim
from IPython.display import HTML
HTML('<center><img src="media/Orbita_rodo.png" width="30%"></center>')
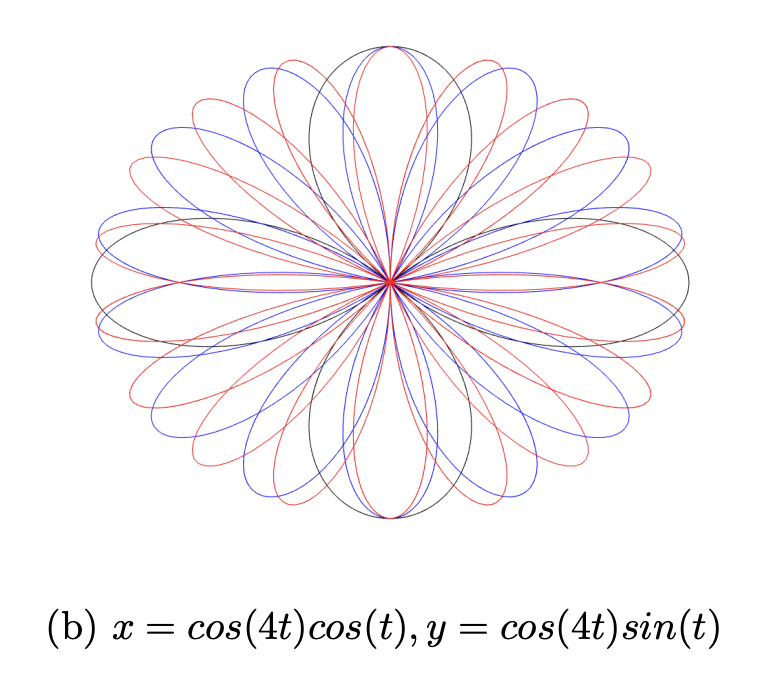
// 6_Curva rodonea
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg ratio=#[1,2],freq=#[227,258], r=1,rota=0,
amp=0.2,gate=0,pan=0,done=2;
var phs, n, rho, pol, cx,cy, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi) * ratio[1]; // phs * denominatore
n = ratio[0]/ratio[1]; // Ratio
rho = cos(n * phs); // Calcola il rho
phs = phs + (rota*2pi); // Rotazione
x = rho * sin(phs) ; // Da polare a cartesiano
y = rho * cos(phs); // Da polare a cartesiano
cx = MouseX.kr(-1, 1.0); // Origine x
cy = MouseY.kr(-1, 1.0); // Origine y
x = r * x + cx;
y = r * y + cy;
[x,y].scope; // Metti visualizzazione XY
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\ratio, [2,4],\r,0.5,\freq,[200,200],\gate,1])
a.set(\r,0.3,\rota,0.1);
a.set(\ratio, [2,4])
a.set(\ratio, [rrand(1,10),rrand(1,10)],\r,0.5)
a.release;
//------------------------------------------------------------------
// Noise
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=400,amp=0,gate=0,pan=0,done=2;
var phs,r,offph, cx,cy,x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFNoise2.ar(freq).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = MouseY.kr(0, 1); // Raggio
offph = MouseX.kr(0,pi); // Defasaggio
cx = MouseX.kr(-1, 1.0); // Origine di x
cy = MouseY.kr(-1, 1.0); // Origine di y
x = r * sin(phs) + cx;
y = r * cos(phs + offph) + cy;
[x,y].scope;
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.release;
//------------------------------------------------------------------
// Ellittica...
// Vedi WT_5.png ... con battimenti stereo...
(
f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // C.Roads
SynthDef.new(\wts_3, {arg freq=#[200,201],amp=0,gate=0,pan=0,done=2;
var phs,r,offph, cx,cy,x, y, sig, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = MouseY.kr(0, 1); // Raggio
offph = MouseX.kr(0,pi); // Defasaggio
cx = MouseX.kr(-1, 1.0); // Origine x
cy = MouseY.kr(-1, 1.0); // Origine y
x = r * sin(2pi * phs + (pi/5)) + cx;
y = r * sin(2pi * phs) + cy;
[x,y].scope;
// ------------------------------
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_3,[\amp,0.2,\gate,1])
a.set(\r,0.6);
a.set(\freq, [rrand(200,205),rrand(200,205)])
a.release;
// Musicalmente qualsiasi superficie tridimensionale può essere utilizzata
// come Wave Terrain sia quelle costruite attraverso funzioni matematiche,
// sia derivate da proiezioni topografiche arbitrarie come una mappa di rilievi
// di una determinata regione geografica.
// Devono però seguire due regole:
//
// --> x e y devono essere entrambe comprese tra -1 e +1
// --> le funzioni d'onda che generano x e y devono produrre valori continui
// (in senso matematico) sul terreno
// --> x e y devono avere valore 0.0 ai limiti del terreno esattamente come
// l'inizio e la fine delle wavetables bidimensionali.
//
// https://www.wolframalpha.com/
(
//f = {arg x, y; (x - y) * (x - 1) * (x + 1) * (y - 1) * (y + 1)}; // Roads
f = {arg x, y; (sin(x) + sin(y)).sqrt/2}; // lepoard function
// f = {arg x, y; sin(2pi*x) * sin(2*pi*y)}; // WT_5.png
// f = {arg x, y; (5/3)*(x-y)*((x*x)-1)*((y*y)-1)}; // Stuart G. James
// f = {arg x, y; sin(pow(x+1, 4)*2pi)*sin(pow(y+1, 4)*2pi)}; // Mills, A. and R. C. De Souza.
// f = {arg x, y; sin(x*2pi+ 3*sin(y*2pi))}; // Modulazione di fase
// f = {arg x, y; sin(pow(3*x,2) + pow(3*y,3))}; // Stuart G. James
// f = {arg x, y; cos(sin(12*x*y)/(pow(x,2) + pow(y,2)))};
// f.plot;
SynthDef.new(\wts_3, {arg ratio=#[1,2],freq=#[200,201],amp=0,gate=0,pan=0,done=2;
var phs,r,offph, cx,cy,x, y, sig, env;
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = MouseY.kr(0, 1);
// r = SinOsc.kr(MouseY.kr(0.5,4)).unipolar; // KSig..
offph = MouseX.kr(0,pi); // Defasaggio
// offph = SinOsc.kr(MouseX.kr(0.5,4)).range(0,pi); // KSig...
cx = MouseX.kr(-1, 1.0); // trasla l'origine di x
cy = MouseY.kr(-1, 1.0); // trasla l'origine di y
x = r * cos(ratio[0]*phs)*cos(phs) + cx; // Orbita a fiore....
y = r * cos(ratio[1]*phs)*sin(phs) + cy;
[x,y].scope;
sig = Limiter.ar(f.value(x, y));
env = Linen.kr(gate,doneAction:done);
sig = LeakDC.ar(sig);
sig = Pan2.ar(sig*env*amp,pan);
Out.ar(0,sig)
}).add;
)
x.free;
// ===========================================================
// Come per la waveshaping un'altro metodo (meno costoso a
// livello computazionale) consiste nel memorizzare in due
// Buffers i profili d'onda x e y per poi rileggerli con
// due segnali puntatori (orbite)
(
s.boot;
s.scope;
s.freqscope;
{s.plotTree}.defer(2)
)
(
Buffer.freeAll;
~bx = Buffer.alloc(s, 1024, 1);
~bx.sine1([1],true,false); // No wavetable format
~by = Buffer.alloc(s, 1024);
~by.sine1([1,6,9],true,false); // No wavetable format
)
~bx.plot;
~by.plot;
(
SynthDef.new(\wts_2, {arg bufx=b,bufy=c,freq=#[400,410],amp=0,gate=0,pan=0,done=2;
var phs,r, offph,cx,cy,x, y, sig, sigx, sigy, env;
// ------------------------------ Orbite (tra -1 e +1)
phs = LFSaw.ar(freq, -1).range(0, 2pi); // Tra 0 e 2pi (angolo giro)
r = LFNoise1.kr(0.4).unipolar; // Raggio
offph = LFNoise1.kr(0.4).range(0,pi); // Defasaggio
cx = LFNoise1.kr(1.3); // origine x
cy = LFNoise1.kr(0.5); // origine y
x = r * sin(phs) + cx;
y = r * cos(phs + offph) + cy;
[x,y].scope;
// ------------------------------
sigx = BufRd.ar(1,bufx, x.range(0,BufFrames.kr(bufx))); // Tra 0 e n-1
sigy = BufRd.ar(1,bufy, y.range(0,BufFrames.kr(bufy)));
sig = sigx * sigy;
env = Linen.kr(gate,doneAction:done);
sig = Pan2.ar(sig*env*amp,pan);
sig = LeakDC.ar(sig);
Out.ar(0,sig)
}).add;
)
a = Synth.new(\wts_2, [\bufx,~bx,\bufy,~by,\freq,[200,201],\amp,0.5,\gate,1]);
a.set(\freq, [100,101])
a.release;